미적분학의기본정리,FTC

Redirected from page "미적분학의기본정리,FTC"
AKA: 미분적분학의 기본 정리, 미적분의 기본 정리, Fundamental Theorem of Calculus, FTC

적분한 다음 미분하면 원래 함수가 되고
미분한 다음 적분하면 원래 함수가 되고 이거? CHK

연속함수 $f(x)$ 에 대해 다음 등식이 성립
$\frac{d}{dx}\int_a^xf(t)dt=f(x)$
다른 형태
$\lim_{x\to a}\frac1{x-a}\int_a^xf(t)dt=f(a)$
$\lim_{h\to0}\frac1h\int_a^{a+h}f(t)dt=f(a)$

[edit]

Definition

함수 $f$ 가 닫힌 구간 $[a,\,b]$ 에서 연속함수일 때,
$[a,\,b]$ 에 속하는 모든 $x$ 에 대하여,
$F^{\prime}(x)=f(x)$ 이면 다음 두 식이 성립.

$1.\quad\quad\int_a^b f(x)dx = \left[F(x)\right]_a^b = F(b)-F(a)$

$2.\quad\quad\frac{d}{dx}\int_{u_1(x)}^{u_2(x)}f(t)dt = f\left(u_2(x)\right)u_2^{\prime}(x)-f\left(u_1(x)\right)u_1^{\prime}(x)$

두번째 식의 특별한 경우,
$\frac{d}{dx}\int_{a}^{x}f(t)dt = f(x)\cdot1 - f(a)\cdot 0 = f(x)$

두번째 식의 유도.
아래끝을 상수 $a,$ 위끝을 함수 $v$ 라 하면
$\frac{d}{dx}\int_a^{v(x)}f(t)dt=f(v(x))\cdot v'(x)$
아래끝을 함수 $u,$ 위끝을 상수 $a$ 라 하면
$\frac{d}{dx}\int_{u(x)}^{a} f(t)dt = -\frac{d}{dx}\int_a^{u(x)}f(t)dt=-f(u(x))\cdot u'(x)$
정리
$\int_{u(x)}^{v(x)}f(t)dt=\int_{u(x)}^a f(t)dt + \int_a^{v(x)}f(t)dt$
에 따라 위 둘을 결합하면 [https]FTC and Chain Rule Formula:
$\frac{d}{dx}\int_{u(x)}^{v(x)} f(t)dt = f(v(x))v'(x) - f(u(x))u'(x)$

[edit]

Stewart

Suppose $f$ is continuous on $[a,b].$

1. If $g(x)=\textstyle\int_a^x f(t)dt,$ then $g'(x)=f(x).$

2. $\textstyle\int_a^b f(x)dx=F(b)-F(a),$ where $F$ is any antiderivative of $f,$ that is, $F'=f.$

i.e.

$1.\;\frac{d}{dx}\int_a^x f(t)dt=f(x)$

$2.\;\int_a^b F'(x)dx=F(b)-F(a)$

[edit]

Thomas

[edit]

FTC 1 : 미적분학의 제 1 기본정리

$f$ 가 $[a,b]$ 위에서 연속이면
$F(x)=\int_a^x f(t)dt$
는
  • $[a,b]$ 에서 연속이고
  • $(a,b)$ 에서 미분가능이고
  • 그 도함수는 $f(x)$ 이다.

$F'(x)=\frac{d}{dx}\int_a^x f(t)dt=f(x)$

[edit]

FTC 2 : 미적분학의 제 2 기본정리 (계산 정리)

$f$ 가 $[a,b]$ 의 각 점에서 연속이고
$F$ 를 $[a,b]$ 에서 $f$ 의 역도함수라고 하면
$\int_a^b f(x)dx=F(b)-F(a)$

[edit]

순변화정리(net change theorem)

(제 2 기본정리의 다른 해석)
미분가능한 함수 $F(x)$ 의 구간 $a \le x \le b$ 에서의 순 변화량(net change)은 변화율의 적분이다.
$F(b)-F(a)=\int_a^b F'(x)dx$

[edit]

수학백과의 설명

1. 함수 $f$ 가 구간 $[a,b]$ 에서 연속이고,
$g(x)=\int_a^x f(t)dt$
이면
$g'(x)=f(x)$
이다.

2. 함수 $F$ 의 도함수가 적분가능하면,
$\int_a^b F'(x)dx=F(b)-F(a)$
이다.


[edit]

Proof 1 : do not trust; 비디오 화질이 안좋아서 RE CHK


Theorem

1. 구간 $[a,b]$ 에서 $F'(x)=f(x)$ 이면
$\int_a^bf(x)dx=\left[F(x)\right]_a^b=F(b)-F(a)$
2.
$\frac{d}{dx}\int_a^x f(t)\, dt=f(x)$

Proof

구간 $[a,\,b]$ 를 $n$ 등분. $a=x_0<x_1<x_2<\cdots<x_{n-1}<x_n=b$

$F(b)-F(a) = F(x_n)-F(x_0)$
$=F(x_n)-F(x_{n-1})+F(x_{n-1})-F(x_{n-2})+F(x_{n-2})-\cdots$
$\cdots-F(x_1)+F(x_1)-F(x_0)$
두개 씩 묶으면
$=\sum_{i=1}^{n}\left(F(x_i)-F(x_{i-1})\right)$

$[a,\,b]$ 위에서 $F'(x)=f(x)$ 이므로
$F$ 는 구간 $[x_{i-1},\,x_i]$ 에서 연속이고
$F$ 는 구간 $(x_{i-1},\,x_i)$ 에서 미분가능하다.
여기서 $i=1,2,\cdots,n$
평균값정리,mean_value_theorem,MVT에 의해
$\frac{F(x_i)-F(x_{i-1})}{x_i-x_{i-1}}=F'(x_i^{*})$ 여기서, $x_{i-1}\le x_i^{*}\le x_i$
$\Leftrightarrow F(x_i)-F(x_{i-1})=F'(x_i^{*})(x_i-x_{i-1})=f(x_i^{*})\Delta x$

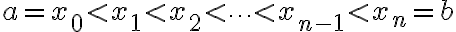
∴ $F(b)-F(a)=\sum_{i=1}^{n}f(x_i^{*})\Delta x$
좌변은 상수, 우변은 리만합
양변에 극한을 취하면
$\lim_{n\to\infty}(F(b)-F(a))= \lim_{n\to\infty}\sum_{i=1}^nf(x_i^{*})\Delta x=\int_a^bf(x)dx$

[edit]

Proof 2

먼저 적분에 관한 평균값 정리

함수 f가 닫힌 구간 [a,b]에서 연속이면 구간 [a,b] 안에 적어도 한 점 c가 존재해서 다음을 만족.
$f(c)=\frac1{b-a}\int_a^bf(x)dx$

평균,mean,average에 똑같은 식 나옴
증명

극값정리에 의하여
$\exists \alpha,\beta\in[a,b]$ such that $f(\alpha)\le f(x)\le f(\beta),\quad\forall x\in[a,b]$
☞
$\int_a^bf(\alpha)dx\le\int_a^bf(x)dx\le\int_a^bf(\beta)dx$
☞
$f(\alpha)(b-a) \le\int_a^bf(x)dx\le f(\beta)(b-a)$

∵
$f(\alpha)\le \frac1{b-a}\int_a^bf(x)dx \le f(\beta)$

중간값정리에 의하여
$\exists c \in [a,b]$
such that
$f(c)=\frac1{b-a}\int_a^bf(x)dx \quad \qed$

[edit]

etc

위의 것은 1차원이고, 2차원의 경우 Stokes' theorem이라 하고 3차원의 경우 Gauss' theorem이라고 하는데 이것들을 통틀어 Generalized FTC라고도 한다.
출처: https://goo.gl/ZFiETA

FTC의 심화버전인 발산정리,divergence_theorem와 스토크스_정리,Stokes_theorem는 각각 2차원 곡면/1차원 곡선에서 벡터함수의 적분을 해당 함수를 미분하여 3차원 공간/2차원 곡면에서 적분하는 것으로 바꿀 수 있다는 것을 의미한다. Namu:미적분학#s-3.2 CHK

FTC는 macroscopic - microscopic 연산을 이어주는 다리,
그린_정리,Green_theorem는 이 관계를 2변수함수로 확장한 것,
스토크스_정리,Stokes_theorem와 발산정리,divergence_theorem는 이 관계를 3변수함수로 확장한 것,
일반화(된)_스토크스_정리 generalized_Stokes_theorem { WpEn:Generalized_Stokes_theorem }은 이 관계를 함수를 너머 추상적인 것으로 확장한 것.
"스토크스 정리"의 정확한 이름이 "켈빈-스토크스 정리"이며, "일반화된 스토크스 정리"의 정확한 이름이 "스토크스 정리"
(src https://dimenchoi.tistory.com/42)