면적적분(면적분,surface_integral)과 체적적분을 연결?
한국어 글 (2차원)
https://angeloyeo.github.io/2020/08/19/divergence_theorem_2D.html
3차원 발산 정리(가우스 정리)
https://angeloyeo.github.io/2020/08/23/divergence_theorem_3D.html
https://angeloyeo.github.io/2020/08/19/divergence_theorem_2D.html
3차원 발산 정리(가우스 정리)
https://angeloyeo.github.io/2020/08/23/divergence_theorem_3D.html
관련:
플럭스 (curr goto 선속,flux)
벡터장,vector_field의 발산,divergence, 선적분,line_integral, 면적분,surface_integral 등 중적분,multiple_integral, 즉 벡터미적분,vector_calculus
그린_정리,Green_theorem
스토크스_정리,Stokes_theorem에 발산정리와의 비교 있음
벡터장,vector_field의 발산,divergence, 선적분,line_integral, 면적분,surface_integral 등 중적분,multiple_integral, 즉 벡터미적분,vector_calculus
그린_정리,Green_theorem
스토크스_정리,Stokes_theorem에 발산정리와의 비교 있음
Sadiku 3.6 p79 ¶
AKA Gauss-Ostrogradsky 정리
발산정리는 폐곡면 S를 통해 나가는 벡터장  의 총 선속은
의 총 선속은  의 발산을 체적적분한 것과 같다는 것을 의미한다.
의 발산을 체적적분한 것과 같다는 것을 의미한다.
정길수 ¶
포장지로 포장했을 때
포장지를 통해 표면으로 나오는 양은
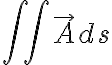
즉 면적분은 곡면에서 유출되는 양.
단위 입체에서 순 유출되는 양은
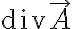 이므로
이므로
전체에서 유출되는 양은
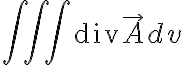
가우스의 발산정리는
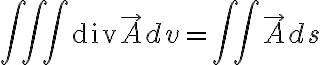
포장지를 통해 표면으로 나오는 양은
단위 입체에서 순 유출되는 양은
ghebook ¶
발산,divergence 연산자를 체적적분,volume_integral에 적용하면 발산정리,divergence_theorem 혹은 가우스_정리,Gauss_s_theorem를 얻을 수 있다.
Thomas ¶
벡터장 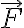 의 성분함수가 연속인 1계 편도함수를 갖고,
의 성분함수가 연속인 1계 편도함수를 갖고,
 가 방향을 갖는 구분적으로 매끄러운 닫힌 곡면이라고 하자.
가 방향을 갖는 구분적으로 매끄러운 닫힌 곡면이라고 하자.
이 곡면의 외향 법선 벡터장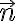 의 방향으로 곡면
의 방향으로 곡면  를 통과하는 벡터장
를 통과하는 벡터장 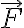 의 유출은
의 유출은
이 곡면이 둘러싸는 영역 위에서
위에서 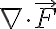 의 적분과 같다.
의 적분과 같다.
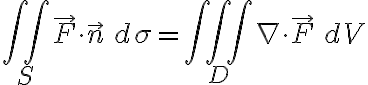
(위 식은 (외향 유출) = (발산적분))
이 곡면의 외향 법선 벡터장
이 곡면이 둘러싸는 영역
(Thomas 13e ko chap14.8 발산정리와 통합 이론 - 정리 8)
tmp ¶
발산의 정리:
즉 면적분과 체적적분을 변환할 수 있다?
즉 면적분과 체적적분을 변환할 수 있다?
![[https]](/123/imgs/https.png) 수학백과: 발산정리
수학백과: 발산정리![[https]](/123/imgs/https.png) 물리학백과: 다이버전스 정리 // 이상은 개론만
물리학백과: 다이버전스 정리 // 이상은 개론만https://ncatlab.org/nlab/show/divergence theorem
Up: 벡터미적분,vector_calculus

