AKA: 미분적분학의 기본 정리, 미적분의 기본 정리, Fundamental Theorem of Calculus, FTC
적분한 다음 미분하면 원래 함수가 되고
미분한 다음 적분하면 원래 함수가 되고 이거? CHK
미분한 다음 적분하면 원래 함수가 되고 이거? CHK
연속함수 ) 에 대해 다음 등식이 성립
에 대해 다음 등식이 성립
dt=f(x))
다른 형태
dt=f(a))
dt=f(a))
Proof 1 : do not trust; 비디오 화질이 안좋아서 RE CHK ¶
Theorem
1. 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서
에서 =f(x)) 이면
이면
![$\int_a^bf(x)dx=\left[F(x)\right]_a^b=F(b)-F(a)$ $\int_a^bf(x)dx=\left[F(x)\right]_a^b=F(b)-F(a)$](/123/cgi-bin/mimetex.cgi?\Large \int_a^bf(x)dx=\left[F(x)\right]_a^b=F(b)-F(a))
2.
\, dt=f(x))
Proof
구간 ![$[a,\,b]$ $[a,\,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,\,b]) 를
를 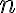 등분.
등분. 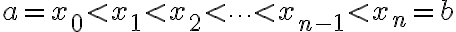
∴ -F(a)=\sum_{i=1}^{n}f(x_i^{*})\Delta x)
좌변은 상수, 우변은 리만합
양변에 극한을 취하면
-F(a))= \lim_{n\to\infty}\sum_{i=1}^nf(x_i^{*})\Delta x=\int_a^bf(x)dx)
좌변은 상수, 우변은 리만합
양변에 극한을 취하면
etc ¶
위의 것은 1차원이고, 2차원의 경우 Stokes' theorem이라 하고 3차원의 경우 Gauss' theorem이라고 하는데 이것들을 통틀어 Generalized FTC라고도 한다.
출처: https://goo.gl/ZFiETA
출처: https://goo.gl/ZFiETA
FTC의 심화버전인 발산정리,divergence_theorem와 스토크스_정리,Stokes_theorem는 각각 2차원 곡면/1차원 곡선에서 벡터함수의 적분을 해당 함수를 미분하여 3차원 공간/2차원 곡면에서 적분하는 것으로 바꿀 수 있다는 것을 의미한다.  미적분학#s-3.2 CHK
미적분학#s-3.2 CHK
FTC는 macroscopic - microscopic 연산을 이어주는 다리,
그린_정리,Green_theorem는 이 관계를 2변수함수로 확장한 것,
스토크스_정리,Stokes_theorem와 발산정리,divergence_theorem는 이 관계를 3변수함수로 확장한 것,
일반화(된)_스토크스_정리 generalized_Stokes_theorem { Generalized_Stokes_theorem }은 이 관계를 함수를 너머 추상적인 것으로 확장한 것.
Generalized_Stokes_theorem }은 이 관계를 함수를 너머 추상적인 것으로 확장한 것.
"스토크스 정리"의 정확한 이름이 "켈빈-스토크스 정리"이며, "일반화된 스토크스 정리"의 정확한 이름이 "스토크스 정리"
(src https://dimenchoi.tistory.com/42)
그린_정리,Green_theorem는 이 관계를 2변수함수로 확장한 것,
스토크스_정리,Stokes_theorem와 발산정리,divergence_theorem는 이 관계를 3변수함수로 확장한 것,
일반화(된)_스토크스_정리 generalized_Stokes_theorem {
"스토크스 정리"의 정확한 이름이 "켈빈-스토크스 정리"이며, "일반화된 스토크스 정리"의 정확한 이름이 "스토크스 정리"
(src https://dimenchoi.tistory.com/42)
![[http]](/123/imgs/http.png) 수학산책: 미적분의 기본정리
수학산책: 미적분의 기본정리https://everything2.com/title/Fundamental theorem of calculus
https://ncatlab.org/nlab/show/fundamental theorem of calculus


![[https]](/123/imgs/https.png)