선형종속,linear_dependence

선형종속,linear_dependence (rev. 1.4)

[edit]

1. tmp 1

[edit]

1.1. 벡터의 선형독립과 선형종속

벡터공간,vector_space 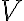$V$ 의 부분집합,subset 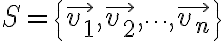$S=\left\{ \vec{v_1},\vec{v_2},\cdots,\vec{v_n} \right\}$ 의 선형결합,linear_combination이 0일 때, 즉
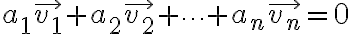$a_1\vec{v_1}+a_2\vec{v_2}+\cdots+a_n\vec{v_n}=0$ ....// 이거 우변 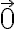$\vec{0}$ 아닌지? 아님 상관없는건지?
일 때 이를 만족시키는 해,solution가
$a_1=a_2=\cdots=a_n$
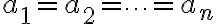
밖에 존재하지 않으면,(그럼 존재성,existence ∩ 유일성,uniqueness?) 벡터 집합 $S$ 는 (안의 벡터들이 서로pairwise? chk) 선형독립,linear_independence이라 하고
그렇지 않으면 선형종속,linear_dependence이라 한다.

벡터 집합이 주어졌을 때,
  • 어떤 벡터를 다른 벡터들의 선형결합으로 쓸 수 있으면 선형종속
  • 어떤 벡터를 다른 벡터들의 선형결합으로 쓸 수 없으면 선형독립

여기서 해가
$a_1=a_2=\cdots=a_n=0$
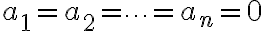
인 경우가 바로 자명해,trivial_solution라고. (선형독립의 특수한 경우? chk)

[edit]

1.2. 행렬,matrix의 선형독립과 선형종속

열벡터,column_vector $\vec{a_n}=\begin{bmatrix}a_{1n}\\a_{2n}\\ \vdots \\ a_{nn}\end{bmatrix}$ 들로 이루어진 행렬 $A=\begin{bmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{bmatrix}$ 에 대해,
열벡터들 $\vec{a_1},\vec{a_2},\cdots,\vec{a_n}$ 이 (pairwise?)
선형독립일 필충조건 : $\det A = |A| \ne 0$
선형종속일 필충조건 : $\det A = |A| = 0$

[edit]

2. tmp 2




Compare: 선형독립,linear_independence <- curr see there. 저기를 봐도 ok. 서로 complement 관계이니