1. tmp 0 from KUIAI ¶
- 집합 S가 선형종속일 필요충분조건은, S에 속하는 한 벡터가 다른 벡터들의 선형결합으로 표시되는 것.
- 집합 S가 영벡터를 포함하면 S는 선형종속.
- 집합 S의 부분집합 S'이 선형종속이면 S도 선형종속이며, S가 선형독립이면 S'도 선형독립.
2.1. 벡터,vector의 선형독립과 선형종속 ¶
벡터공간,vector_space 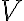 의 부분집합,subset
의 부분집합,subset 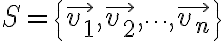 의 선형결합,linear_combination이 0일 때, 즉
의 선형결합,linear_combination이 0일 때, 즉
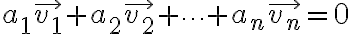 ....// 이거 우변
....// 이거 우변 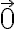 아닌지? 아님 상관없는건지?
아닌지? 아님 상관없는건지?
일 때 이를 만족시키는 해,solution가
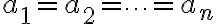 ....=0 이 빠진듯
....=0 이 빠진듯
밖에 존재하지 않으면,(그럼 존재성,existence ∩ 유일성,uniqueness?) 벡터 집합  는 (안의 벡터들이 서로pairwise? chk) 선형독립,linear_independence이라 하고
는 (안의 벡터들이 서로pairwise? chk) 선형독립,linear_independence이라 하고
그렇지 않으면 선형종속,linear_dependence이라 한다.
그렇지 않으면 선형종속,linear_dependence이라 한다.
벡터 집합이 주어졌을 때,
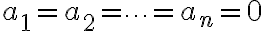
인 경우가 바로 자명해,trivial_solution라고. (선형독립의 특수한 경우? chk)
- 어떤 벡터를 다른 벡터들의 선형결합으로 쓸 수 있으면 선형종속
- 어떤 벡터를 다른 벡터들의 선형결합으로 쓸 수 없으면 선형독립
2.2. 행렬,matrix의 선형독립과 선형종속 ¶
2.3. 함수,function의 선형독립과 선형종속 ¶
함수들이 선형결합되어있을 때 그 계수,coefficient들이 모두 0인 자명해,trivial_solution만을 가져야 선형결합=0인 식을 만족한다면 선형독립,linear_independence이다, 라는 것이 여기서도 동일하게 적용된다.
함수들(혹시 함수 집합 이라 해야 정확??) ,f_2(x),\cdots,f_n(x)) 에 대해 상수들
에 대해 상수들 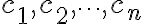 이 존재할 때 이들의 선형결합
이 존재할 때 이들의 선형결합
+c_2f_2(x)+\cdots+c_nf_n(x)=0)
을 만족하는 해가 오직 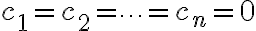 뿐이면, 함수들
뿐이면, 함수들 ,f_2(x),\cdots,f_n(x)) 는 선형독립,linear_independence이다.
는 선형독립,linear_independence이다.
(그렇지 않은 해가 있다면? chk), 함수들,f_2(x),\cdots,f_n(x)) 는 선형종속,linear_dependence이다.
는 선형종속,linear_dependence이다.
(그렇지 않은 해가 있다면? chk), 함수들
4. tbw ¶
대상이 두 개일 경우, 상수배(=스칼라배?)와 밀접한데... tbw.
// tmp from 이종광 공수1 http://kocw.net/home/search/kemView.do?kemId=1215229 7-1 15m
{ // 이건 함수일경우, 그리고 대상이 두 개일 경우인데, del ok
두 함수 와 적당한 상수
와 적당한 상수  에 대해
에 대해
)
을 만족하면 1차 종속이라 하고,
이 같은 가 없으면 1차 독립. (선형독립,linear_independence)
가 없으면 1차 독립. (선형독립,linear_independence)
// tmp from 이종광 공수1 http://kocw.net/home/search/kemView.do?kemId=1215229 7-1 15m
{ // 이건 함수일경우, 그리고 대상이 두 개일 경우인데, del ok
두 함수
이 같은
즉 상수 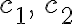 에 대하여
에 대하여
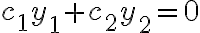
을 만족하는 경우가 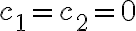 밖에 없으면 두 함수는 1차 독립이라 한다.
밖에 없으면 두 함수는 1차 독립이라 한다.
}
}
Compare/opp: 선형독립,linear_independence <- curr see there. 저기를 봐도 ok. 서로 complement 관계이니


![[https]](/123/imgs/https.png)