1. ? ¶
유클리드_공간,Euclidean_space의 임의의 점의 위치의 좌표/...를 나타낼 때
x축 방향으로의 벡터는 기저,basis(단위벡터,unit_vector, 표준기저,standard_basis)의 실수배 으로 나타낼 수 있다.
으로 나타낼 수 있다.
그런데 이걸로 x축(수직선)에서 벗어난 평면 위 벡터나, y축 방향으로의 벡터를 나타낼 수 없다. 에 무엇을 곱해도 얻을 수 없다. y축 방향으로의 벡터는 반드시
에 무엇을 곱해도 얻을 수 없다. y축 방향으로의 벡터는 반드시  가 필요하다. 이것은
가 필요하다. 이것은  가
가  과 독립이기 때문.
과 독립이기 때문.
평면에서 벗어난 3D 공간의 임의의 좌표도 만으로 나타낼 수 없다. 이때는 반드시
만으로 나타낼 수 없다. 이때는 반드시  가 필요하다.
가 필요하다.
x축 방향으로의 벡터는 기저,basis(단위벡터,unit_vector, 표준기저,standard_basis)의 실수배
그런데 이걸로 x축(수직선)에서 벗어난 평면 위 벡터나, y축 방향으로의 벡터를 나타낼 수 없다.
평면에서 벗어난 3D 공간의 임의의 좌표도
Formal하게는,
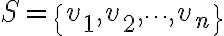 linearly dependent (선형종속,linear_dependence)
linearly dependent (선형종속,linear_dependence)
⇔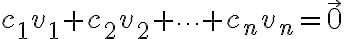 for some
for some 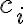 's not all are zero(at least one is non-zero)
's not all are zero(at least one is non-zero)
모두 0이 아닌(적어도 하나가 0이 아닌) 어떤 계수들의 집합에 대해, 선형결합하니 영벡터가 된다
⇔
모두 0이 아닌(적어도 하나가 0이 아닌) 어떤 계수들의 집합에 대해, 선형결합하니 영벡터가 된다
이것은 equivalently, 한 벡터 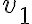 을 다른 벡터들
을 다른 벡터들 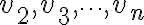 의 선형결합으로 나타낼 수 있다는 것과 동치이다. 보이는 것은 매우 간단하다. 식으로 나타내면
의 선형결합으로 나타낼 수 있다는 것과 동치이다. 보이는 것은 매우 간단하다. 식으로 나타내면
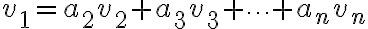 인데, 좌변에 있는 것을 이항하면
인데, 좌변에 있는 것을 이항하면
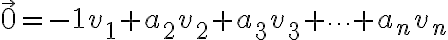
인데 우변의 즉 non-zero 계수가 있음을 볼 수 있다.
즉 non-zero 계수가 있음을 볼 수 있다.
인데 우변의
위의 식
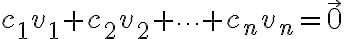
에서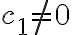 으로 가정하면
으로 가정하면
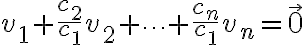
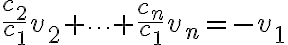
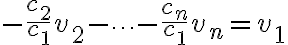
이므로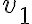 이 다른 벡터들의 선형결합으로 나타남을 볼 수 있다.
이 다른 벡터들의 선형결합으로 나타남을 볼 수 있다.
에서
이므로
예를 들어 벡터 집합
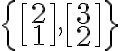
에서 선형결합
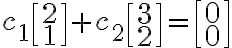
을, 즉 선형결합해서 영벡터를 만드는 경우가
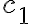 or
or 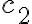 nonzero → 종속(dependent) - 계수가 모두 0인 것이 아닌 어떤 정교한 조합방법이 있으면, (벡터 집합의 원소들이 서로? / 저 집합이?) 선형종속 linearly dependent
nonzero → 종속(dependent) - 계수가 모두 0인 것이 아닌 어떤 정교한 조합방법이 있으면, (벡터 집합의 원소들이 서로? / 저 집합이?) 선형종속 linearly dependent
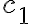 and
and 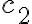 both zero → 독립(independent) - 계수가 모두 0인 경우밖에 없으면 (벡터 집합의 원소들이 서로? / 저 집합이?) 선형독립 linearly independent
both zero → 독립(independent) - 계수가 모두 0인 경우밖에 없으면 (벡터 집합의 원소들이 서로? / 저 집합이?) 선형독립 linearly independent
이 예의 경우는 다음 선형방정식,linear_equation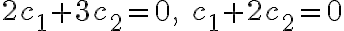 을 풀면
을 풀면 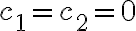 인 경우밖에 없으므로 선형독립이다.
인 경우밖에 없으므로 선형독립이다.
그리고 이 벡터들의 생성이 이다.
이다.
이 예의 경우는 다음 선형방정식,linear_equation
그리고 이 벡터들의 생성이
(Khan)
//수백
{
벡터공간,vector_space의 부분집합,subset의 선형결합,linear_combination이 영벡터,zero_vector인 경우가, 계수가 모두 0인 자명한 경우밖에 없으면 선형독립이고, 그렇지 않으면 선형종속.
i.e.
벡터공간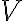 의 부분집합
의 부분집합  의 일차결합이 영벡터인 경우, 즉
의 일차결합이 영벡터인 경우, 즉
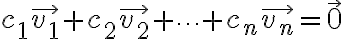
인 경우가
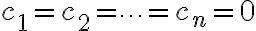
인 경우밖에 없으면 선형독립이며 그렇지 않으면 선형종속.
{
벡터공간,vector_space의 부분집합,subset의 선형결합,linear_combination이 영벡터,zero_vector인 경우가, 계수가 모두 0인 자명한 경우밖에 없으면 선형독립이고, 그렇지 않으면 선형종속.
i.e.
벡터공간
일차독립성의 다른 표현
다음 둘은 동치.
이 일차독립이다.
를 그 나머지 벡터들의 일차결합으로 쓸 수 없다.
이 일차종속(선형종속,linear_dependence)이다.
를 그 나머지 벡터들의 일차결합으로 쓸 수 있다.
CHK (출처 알수없음 종이에 적혀있던거)
요소들 ) 에 대해
에 대해
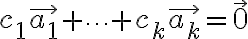
을 만족하는 실수의 조합
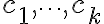 (적어도 이 중 하나는
(적어도 이 중 하나는 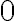 이 아님)
이 아님)
가 존재할 때 이 요소들은 일차종속이다.
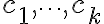 가 모두
가 모두 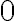 인 경우를 제외하고 위 식을 만족시킬 수 없으면 이 요소들은 일차독립이다.
인 경우를 제외하고 위 식을 만족시킬 수 없으면 이 요소들은 일차독립이다.
생각: 즉 영벡터를 만들 수 있는 방법이 자명한 방법 하나로 유일하면 일차독립, 그게 아니면 일차종속?
일차독립임을 증명하는 방법:
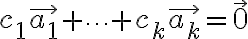 이라는 전제를 두고
이라는 전제를 두고  이면 일차독립.
이면 일차독립.
특정 생성집합(생성,span)으로 유일하게(unique) 벡터를 표현할 수 없을 수도 있다. 예를 들어 ,(0,1),(1,1)\rbrace \in \mathbb{R}^2) 이면
이면 ) 는
는
+2(0,1)+0(1,1))
+0(0,1)+2(1,1))
이므로 표현이 유일하지 않다. 여기서 일차독립=선형독립 개념이 나온다.
Def. (Linearly independent)
Let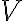 be a vector space and let
be a vector space and let 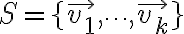 be a subset of
be a subset of 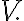 We call
We call 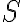 linearly independent if
linearly independent if
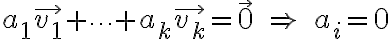
for all 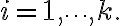
Let
If 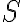 is not linearly independent, we say that
is not linearly independent, we say that 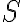 is linearly dependent.
is linearly dependent.
함수 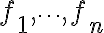
상수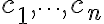 일 때
일 때
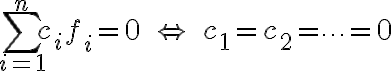
이면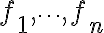 은 linearly independent하고
은 linearly independent하고
아니면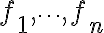 은 linearly dependent하다.
은 linearly dependent하다.
상수
이면
아니면
2. Heinbockel ¶
함수,function 집합,set 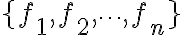 의 선형결합,linear_combination
의 선형결합,linear_combination 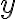 는 상수곱의 합,sum인
는 상수곱의 합,sum인
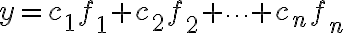
함수의 선형독립/종속 (설명 1)
만약 함수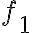 이
이 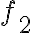 의
의 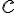 (상수)배이면,
(상수)배이면, =cf_2(x)) 로 쓸 수 있고, 이 경우
로 쓸 수 있고, 이 경우 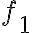 은
은 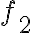 에 선형종속,linear_dependence이다. (원문: linearly dependent upon = 선형으로 의존하는)
에 선형종속,linear_dependence이다. (원문: linearly dependent upon = 선형으로 의존하는)
그런 상수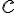 가 없으면, 두 함수는 선형독립,linear_independence이다.
가 없으면, 두 함수는 선형독립,linear_independence이다.
만약 함수
그런 상수
함수의 선형독립/종속 (설명 2)
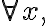 다음 선형결합
다음 선형결합
+c_2f_2(x)=0) ...(1)
...(1)
을 만족하는 0이 아닌(모두 0이 아닌?) 두 상수 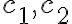 가 존재하면 함수의 집합
가 존재하면 함수의 집합 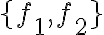 은 종속적인 함수의 집합이라고 한다. (원문: set of dependent functions)
은 종속적인 함수의 집합이라고 한다. (원문: set of dependent functions)
이유: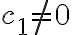 이면,
이면,
=-\frac{c_2}{c_1}f_2(x)=cf_2(x))
이기 때문. 만약 (1)을 참으로 만드는 상수가 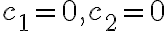 밖에 없으면 함수 집합
밖에 없으면 함수 집합 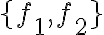 은 선형독립적인 함수의 집합이라고 한다. (원문: set of linearly independent functions)
은 선형독립적인 함수의 집합이라고 한다. (원문: set of linearly independent functions)
이유:
(일반화) 모두 0이 아닌 상수 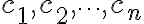 이 있고, 모든
이 있고, 모든 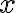 에 대해 선형결합의 값이 0이 되는, 즉
에 대해 선형결합의 값이 0이 되는, 즉
+c_2f_2(x)+\cdots+c_nf_n(x)=0,\;\;\forall x) ...(2)
...(2)
이 되는 모두 0이 아닌 상수들이 있으면, 함수의 집합 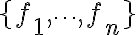 은 선형종속적인 함수의 집합이다. (linearly dependent set of functions) 만약 (2)를 참으로 만드는 상수들이
은 선형종속적인 함수의 집합이다. (linearly dependent set of functions) 만약 (2)를 참으로 만드는 상수들이 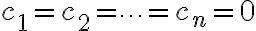 뿐이면, 함수의 집합
뿐이면, 함수의 집합 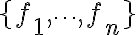 은 선형독립적인 함수의 집합이다.
은 선형독립적인 함수의 집합이다.
함수 집합의 함수들이 선형종속이면, 한 함수는 다른 함수들의 선형결합으로 만들어질(표현될) 수 있다. 예를 들어 (2)에서 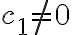 으로 가정하면
으로 가정하면
=-\frac{c_2}{c_1}f_2(x)-\cdots-\frac{c_n}{c_1}f_n(x))
이므로 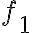 은 다른 함수들에 대해 선형종속이다.
은 다른 함수들에 대해 선형종속이다.
from: Intro to Calculus Volume I p13
4. 벡터방정식 해와의 관계 ¶
벡터방정식,vector_equation이 trivial solution만 가지면 linearly independent.
벡터방정식,vector_equation이 nontrivial solution을 가지면 linearly dependent.
Related: 해,solution
벡터방정식,vector_equation이 nontrivial solution을 가지면 linearly dependent.
Related: 해,solution
5. 함수의 독립 (Zill) ¶
함수의 경우
A set of functions ,f_2(x),\cdots,f_n(x)) is said to be linearly dependent on an interval
is said to be linearly dependent on an interval  if there exist constants
if there exist constants 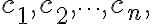 not all zero, such that
not all zero, such that
+c_2f_2(x)+\cdots+c_nf_n(x)=0)
for every 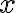 in the interval. If the set of functions is not linearly dependent on the interval, it is said to be linearly independent.
in the interval. If the set of functions is not linearly dependent on the interval, it is said to be linearly independent.
다시 말해, 위 식을 모든 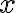 에 대해 만족시키는 상수들이
에 대해 만족시키는 상수들이 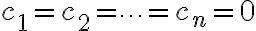 뿐이면, 함수들의 집합이 그 구간에서 선형독립.
뿐이면, 함수들의 집합이 그 구간에서 선형독립.
두 함수가 선형종속이면, 하나는 다른 것의 상수배이다.
+c_2f_2(x)=0) 이면
이면 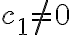 이라는 가정 하에
이라는 가정 하에 =(-c_2/c_1)f_2(x)) 이므로.
이므로.
(Zill 6e Definition 3.1.1 Linear Dependence/Independence)
.....
함수의 선형독립/선형종속은 론스키언,Wronskian과도 관련있음.
론스키언,Wronskian을 계산하여 0인지 여부로 독립 여부를 판별 가능? CHK
Yes, see https://angeloyeo.github.io/2019/10/10/Wronskian.html
함수의 선형독립부터 설명함.
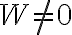 일 때 함수집합이 선형독립적. 하지만 주의할 것은
일 때 함수집합이 선형독립적. 하지만 주의할 것은
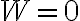 이라고 함수 집합이 항상 선형종속인 것은 아님.
이라고 함수 집합이 항상 선형종속인 것은 아님.
6. 벡터의 독립 (Lay, Zill) ¶
벡터의 경우
An indexed set of vectors 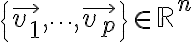 is said to be linearly independent if the vector equation
is said to be linearly independent if the vector equation
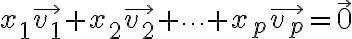
has only the trivial solution. The set 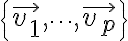 is said to be linearly dependent if there exist weights
is said to be linearly dependent if there exist weights 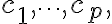 not all zero, such that
not all zero, such that
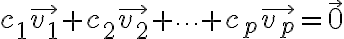
(Lay 1.7: Linear Independence)
An indexed set of vectors 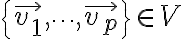 is said to be linearly independent if the vector equation
is said to be linearly independent if the vector equation
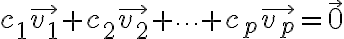 ......(1)
......(1)
has only the trivial solution, 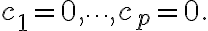
The set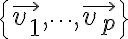 is said to be linearly dependent if (1) has a nontrivial solution, that is, if there are some weights,
is said to be linearly dependent if (1) has a nontrivial solution, that is, if there are some weights, 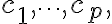 not all zero, such that (1) holds. In such a case, (1) is called a linear dependence relation among
not all zero, such that (1) holds. In such a case, (1) is called a linear dependence relation among 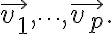
The set
(Lay 4.3: Linearly Independent Sets)
부분공간,subspace 바로 다음에 언급됨.
벡터 집합 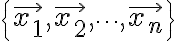 은 다음 방정식
은 다음 방정식
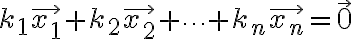
을 만족하는 상수가 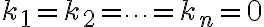 뿐이면 선형독립이다. 선형독립이 아니면 선형종속이다.
뿐이면 선형독립이다. 선형독립이 아니면 선형종속이다.
(Zill Definition 7.6.3 Linear Independence)
7. tmp; 벡터의 선형결합과 선형독립/선형종속 ¶
from 고급수학.pdf p56; CLEANUP
and,
일차독립 and 일차종속
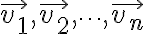
에서 어떤 하나도 나머지 (n-1)개의 일차결합으로 표현될 수 없으면 이 벡터들은 일차독립.
일차독립이 아닐 때 (어느 한 벡터가 나머지 벡터들의 일차결합으로 표현될 수 있을 때) 일차종속.
일차독립이 아닐 때 (어느 한 벡터가 나머지 벡터들의 일차결합으로 표현될 수 있을 때) 일차종속.
8. Kreyszig 7.4 벡터의 1차독립과 종속 ¶
같은 수의 성분을 가진 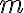 개의 벡터
개의 벡터 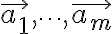 에 대해 이들 벡터의 1차결합(선형결합,linear_combination)이란 임의의 스칼라
에 대해 이들 벡터의 1차결합(선형결합,linear_combination)이란 임의의 스칼라 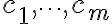 에 대해
에 대해
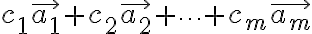
으로 표현된 것을 말한다. 이제 방정식
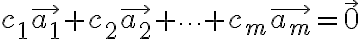 ......(1)
......(1)
을 생각하면, 이 방정식은 모든  의 값이 0일 때 성립한다. 만약 이것이 식 (1)을 만족하는 유일한
의 값이 0일 때 성립한다. 만약 이것이 식 (1)을 만족하는 유일한 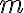 개의 스칼라라면, 벡터
개의 스칼라라면, 벡터 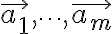 이 1차독립 집합을 형성한다고 말하고, 간단히 이들 벡터를 1차독립(linearly independent)이라고 한다.
이 1차독립 집합을 형성한다고 말하고, 간단히 이들 벡터를 1차독립(linearly independent)이라고 한다.
반면에 모두 0은 아닌 스칼라 집합에 대해서도 식 (1)이 성립한다면, 이 벡터들을 1차종속(linearly dependent)이라고 한다. 왜냐하면 이때에는 벡터 중 최소한 하나 이상을 다른 벡터들의 1차결합으로 나타낼 수 있기 때문이다.
ex. 만일 식 (1)이 성립하고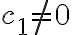 이면, 벡터
이면, 벡터 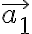 을
을
)
로 나타낼 수 있다. (단 어떤 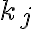 는 0일 수 있으며, 심지어
는 0일 수 있으며, 심지어 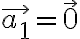 이면 모든
이면 모든 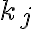 가 0일 수 있다)
가 0일 수 있다)
ex. 만일 식 (1)이 성립하고
(위의 개념들의 중요성): 1차종속인 벡터집합에서, 다른 벡터들의 1차결합으로 표현되는 벡터들을 소거함으로써, 최종적으로 각 벡터들이 나머지 다른 벡터의 1차결합으로는 절대 표현되지 않는, 즉 1차독립인 부분집합을 얻을 수 있다는 것. 이 집합이 결국 우리가 필요로 하는 가장 작은 벡터 집합.
(책에서는 바로 이어서 계수,rank 언급.)
9. tmp: 일차독립 vs 일차종속 : 이석종 ¶
(from 충북대 이석종 미적 강의 https://www.youtube.com/watch?v=5bxNSs4eAig&list=PLhA7rnOc58_xJXXHRHtlkLkgTJCfI-ceX&index=12 중에서)
https://youtu.be/5bxNSs4eAig?t=1367
대충 어떤 벡터의 일차결합으로 다른 벡터를 표현할 수 있는가? 가 주제.
https://youtu.be/5bxNSs4eAig?t=1367
대충 어떤 벡터의 일차결합으로 다른 벡터를 표현할 수 있는가? 가 주제.
(정의 9.18)
(1)  이 일차종속(linearly dependent)이란 방정식
이 일차종속(linearly dependent)이란 방정식

을 만족하면서 적어도 하나는 0이 아닌 실수  이 존재하는 경우를 말한다.
이 존재하는 경우를 말한다.
(2)  이 일차독립(linearly independent)이란 일차종속이 아닌 경우를 말한다. 즉,
이 일차독립(linearly independent)이란 일차종속이 아닌 경우를 말한다. 즉,

이면 항상  이 될 경우 일차독립이다.
이 될 경우 일차독립이다.
(예제 9.19)
(1) 표준단위벡터(i.e. 표준기저,standard_basis)은 일차독립임을 쉽게 확인 가능.
(2) 세 벡터 (1,0) (1,1) (0,1)은 일차종속이다. 1·(1,0) + (-1)·(1,1) + 1·(0,1) = (0,0) 이기 때문.
(3) 영벡터,zero_vector를 포함하고 있는 벡터들은 당연히 일차종속. 왜냐하면 영벡터가 하나라도 있다고 하자. (ex.  에서
에서  이라 하자) 그러면
이라 하자) 그러면

이고, 이 때  의 계수는 0이 아니다.
의 계수는 0이 아니다.
(4) 한 벡터  가 일차독립이 될 필요충분조건은
가 일차독립이 될 필요충분조건은  이다.
이다.
(Why? 인 경우를 생각해보면.)
인 경우를 생각해보면.)
(Why?
(5) 하나의 벡터  의 일차결합은
의 일차결합은  의 형태뿐이다. 따라서
의 형태뿐이다. 따라서  가 일차종속이 될 필요충분조건은
가 일차종속이 될 필요충분조건은  이다.
이다.
(정리 9.21)
서로 직교하는 영이 아닌 벡터들) 은 일차독립이다.
은 일차독립이다.
서로 직교하는 영이 아닌 벡터들
(증명) 실수  에 대해
에 대해

이라고 하자. 이 식의 좌변에  에 대한 내적을 구하면
에 대한 내적을 구하면 ) 에 의해
에 의해
)


그런데  은 영벡터가 아니므로
은 영벡터가 아니므로  이고 따라서
이고 따라서  이다.
이다.
마찬가지로 에 대해 양변에
에 대해 양변에  에 대한 내적을 취하면
에 대한 내적을 취하면  임을 알 수 있다.
임을 알 수 있다.
즉, 이다.
이다.
그러므로 은 일차독립이다.
은 일차독립이다.
마찬가지로
즉,
그러므로
(정리 9.23)
벡터 이 일차종속일 필요충분조건은 어떤
이 일차종속일 필요충분조건은 어떤 ) 가 나머지 벡터들의 일차결합으로 표현되는 것이다.
가 나머지 벡터들의 일차결합으로 표현되는 것이다.
(증명) 이 일차종속이면
이 일차종속이면

를 만족하는 모두 0이 아닌 실수들  이 존재한다. 적당한
이 존재한다. 적당한 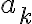 가 0이 아닌 실수라고 하면 (
가 0이 아닌 실수라고 하면 ( 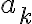 로 양변을 나누어주면 )
로 양변을 나누어주면 )
 {\vec v}_1 + \cdots + \left(-\frac{a_{k-1}}{a_k}\right){\vec v}_{k-1} + \left(-\frac{a_{k+1}}{a_k}\right) {\vec v}_{k+1} + \cdots + \left( -\frac{a_m}{a_k} \right) {\vec v}_m)
으로 표현된다.
따라서 가 나머지 벡터들의 일차결합으로 표현된다.
가 나머지 벡터들의 일차결합으로 표현된다.
벡터
(증명)
따라서
역으로 어떤  가 나머지 벡터들의 일차결합으로 표현된다면
가 나머지 벡터들의 일차결합으로 표현된다면

인 실수들  이 존재한다. 따라서 (
이 존재한다. 따라서 (  를 우변으로 이항하면 )
를 우변으로 이항하면 )

이고 특히  앞의 계수는
앞의 계수는  이다. (따라서 일차종속이다)
이다. (따라서 일차종속이다)
10. tmp links ko ¶
https://rfriend.tistory.com/163
https://junklee.tistory.com/76
https://freshrimpsushi.github.io/posts/linearly-independent-and-linearly-dependent/
https://junklee.tistory.com/76
https://freshrimpsushi.github.io/posts/linearly-independent-and-linearly-dependent/
일차독립, 선형독립, linear independence, linearly independent
일차종속, 선형종속, linear dependence, linearly dependent
일차종속, 선형종속, linear dependence, linearly dependent
Compare: 선형종속,linear_dependence
Related:
선형결합,linear_combination (=일차결합)
선형성,linearity
선형계,linear_system
독립변수와_종속변수
기저,basis
대각화,diagonalization
대각화가능행렬,diagonalizable_matrix
자명해,trivial_solution
선형결합,linear_combination (=일차결합)
선형성,linearity
선형계,linear_system
독립변수와_종속변수
기저,basis
대각화,diagonalization
대각화가능행렬,diagonalizable_matrix
자명해,trivial_solution
Twins:
 일차독립
일차독립
![[https]](/123/imgs/https.png) 수학백과: 일차독립
수학백과: 일차독립
https://mathworld.wolfram.com/LinearlyIndependent.html
https://encyclopediaofmath.org/wiki/Linear_independence
 Linear_independence
Linear_independence
https://en.citizendium.org/wiki/Linear_independence
![[https]](/123/imgs/https.png) 수학백과: 일차독립
수학백과: 일차독립https://mathworld.wolfram.com/LinearlyIndependent.html
https://encyclopediaofmath.org/wiki/Linear_independence
https://en.citizendium.org/wiki/Linear_independence


![[http]](/123/imgs/http.png)