선형근사,linear_approximation와... mklink
함수
점
(Thomas 13e ko 2.11 p141)
Ex ¶
For what values of  is the linear approximation
is the linear approximation
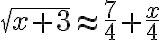
accurate to within 0.5?
Sol.
\right|<0.5)
그래프에서 보면 절대값 안이 항상 음수라 한다.
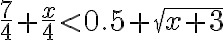
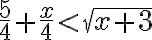
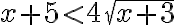
양변을 제곱하면
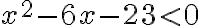
근의 공식을 써서 구간을 구하면

이상 Ex의 source: http://www.kocw.net/home/cview.do?cid=293242 3.11 선형 근사값과 미분
Ex. ¶
Find the linearization of the fn =\sqrt{x+3}) at
at 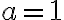 and use it to approximate the numbers
and use it to approximate the numbers 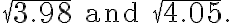 Are these approximations overestimates or underestimates? (더 크게 근사했는가 작게 근사했는가)
Are these approximations overestimates or underestimates? (더 크게 근사했는가 작게 근사했는가)
sol.
The derivative of
=(x+3)^{1/2})
is
=\frac12(x+3)^{-1/2})
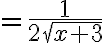
and so we have =2\textrm{ and }f%27(1)=\frac14.)
그리고 L을 구하면, 선형화(linearization)는,
=f(1)+f%27(1)(x-1))
)
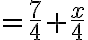
그래서, approximation은,
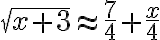
In particular,
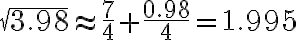
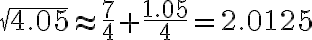
src: KU김기택 강의
The derivative of
그리고 L을 구하면, 선형화(linearization)는,

