순열,permutation

순열,permutation (rev. 1.26)
서로 다른 n개에서 r개를 택하여 일렬로 배열하는 것. (n≥r)

비복원추출 중복 × (불허) 순열 nPr
복원추출 중복 ○ (허락) 중복순열 nΠr=nr

[edit]

순열의 수 계산법

서로 다른 $n$ 개에서 $r$ 개를 택하는 순열의 수는
${}_{n}\mathrm{P}_{r}=\underbrace{n(n-1)(n-2)\cdots(n-(r-1))}_{r\text{ numbers}}\quad\quad(0\lt r\le n)$

계승,factorial을 이용해 표현하면
${}_{n}\mathrm{P}_{r}=\frac{n!}{(n-r)!}\quad\quad(0\le r\le n)$

이유는,
$\frac{n!}{(n-r)!}$
$=\frac{n(n-1)(n-2)\cdots(n-r+1)(n-r)(n-r-1)\cdots 2\cdot 1}{(n-r)(n-r-1)\cdots 2\cdot 1}$
$=n(n-1)(n-2)\cdots(n-r+1)$
$=n(n-1)(n-2)\cdots(n-(r-1))$
$={}_{n}\mathrm{P}_{r}$

그 외 알아두면 좋은 성질들

${}_{n}\mathrm{P}_{n}=n!$

$\left({}_{n}\mathrm{P}_{n}=\frac{n!}{(n-n)!}=\frac{n!}{0!}\right)$

${}_{n}\mathrm{P}_{0}=1$

$\left({}_{n}\mathrm{P}_{0}=\frac{n!}{(n-0)!}\right)$

[edit]

TI-Nspire

nPr(n,r)

[edit]

원순열

서로 다른 n개를 원형으로 배열하는 수는
$\frac{n!}{n}=(n-1)!$

[edit]

중복순열

${}_n\mathrm{\Pi}_r$ 기호는 한국에서만 쓰나?

[edit]

같은 것이 있는 순열

$n$ 개 중 $p$ 개, $q$ 개, $r$ 개, …, $s$ 개가 각각 같은 것일 때,
이들을 일렬로 나열하는 순열의 수는
$\frac{n!}{p!\times q!\times r!\times \cdots \times s!}$
단, $n=p+q+r+\cdots+s$

ex1. 빨간 공 3개, 초록 공 2개, 파란 공 2개를 일렬로 배열하는 방법의 수
$\frac{7!}{3! \cdot 2! \cdot 2!}=210$

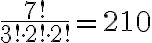
ex2. tomorrow의 8개 알파벳을 일렬로 나열하는 경우의 수는?
sol. o가 세 개, r이 두 개 있으므로
$\frac{8!}{2!\cdot 3!}=3360$

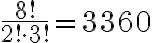
AKA 동자순열, permutation of multisets

[edit]

완전순열 complete permutation

완전순열 complete_permutation = 교란 derangement
rel. 준계승,subfactorial - curr see 계승,factorial
via WpKo:완전순열

[edit]

교대치환, 교대순열 alternating permutation

[edit]

factorial 과의 관계

계승,factorial
순열 = 하강계승 falling_factorial. (namu) QQQ 항상? 완전동의어인지 확실히


[edit]

소스, Prg Lang Impl

----
  • [1] Namu:순열각주 "이 단어는 군론에서 치환을 의미하며"