두 확률변수의 결합확률분포(결합분포)
이산형분포와 연속형분포로 구분 가능
이산형분포와 연속형분포로 구분 가능
1. 이변량 이산형 (결합)분포 ¶
Ex. 동전과 주사위를 동시에 던지는 실험
확률변수 X: 동전의 앞면의 수
확률변수 Y: 주사위의 눈의 수
확률변수 X: 동전의 앞면의 수
확률변수 Y: 주사위의 눈의 수
Ex2. 동전을 세 번 던지는 실험
X: 동전을 처음 두 번 던졌을 때까지 관찰된 앞면의 개수
Y: 세 번 모두 던졌을 때 관찰되는 앞면의 개수
X: 동전을 처음 두 번 던졌을 때까지 관찰된 앞면의 개수
Y: 세 번 모두 던졌을 때 관찰되는 앞면의 개수
각각 가능한 값들:
X = 0, 1, 2
Y = 0, 1, 2, 3
치역 AX×Y = {(x, y) : x = 0, 1, 2; y = 0, 1, 2, 3}Y = 0, 1, 2, 3
표본공간 S 안의 8가지의 가능한 결과는 같은 확률
ex. s = HTH or s = THH
이런 건 이산형 결합분포 (discrete joint distribution) - 확률변수가 두개기 때문에
X와 Y의 결합확률질량함수(joint PMF) - see 결합확률질량함수,joint_probability_mass_function,joint_PMF
ex. s = HTH or s = THH
(X(s), Y(s)) = (1, 2)
![$P[(X,Y)=(1,2)]=P\left{THH,HTH\right}=\frac28$](/123/cgi-bin/mimetex.cgi?\Large P[(X,Y)=(1,2)]=P\left{THH,HTH\right}=\frac28 "$P[(X,Y)=(1,2)]=P\left{THH,HTH\right}=\frac28$")
결합확률분포표:| X\Y | 0 | 1 | 2 | 3 | 계 |
| 0 | 1/8 | 1/8 | 0 | 0 | 2/8 |
| 1 | 0 | 2/8 | 2/8 | 0 | 4/8 |
| 2 | 0 | 0 | 1/8 | 1/8 | 2/8 |
| 계 | 1/8 | 3/8 | 3/8 | 1/8 | 1 |
이런 건 이산형 결합분포 (discrete joint distribution) - 확률변수가 두개기 때문에
X와 Y의 결합확률질량함수(joint PMF) - see 결합확률질량함수,joint_probability_mass_function,joint_PMF
2. 이변량 연속형 분포 ¶
X와 Y의 결합확률밀도함수,joint_probability_density_function,joint_PDF
{
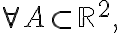
\in A)=\int\int_A f(x,y)dxdy "$P((X,Y)\in A)=\int\int_A f(x,y)dxdy$")
인 음 아닌 함수 
가 존재하면
X와 Y의 분포: 연속형 결합분포(continuous joint distribution)
{
X와 Y의 분포: 연속형 결합분포(continuous joint distribution)
성질
}
ex. c=? P(X≥Y)=?
=\begin{cases}cx^2y,&x^2\le y\le 1\\0,&\textrm{otherwise}\end{cases} "$f(x,y)=\begin{cases}cx^2y,&x^2\le y\le 1\\0,&\textrm{otherwise}\end{cases}$")
sol.
Let 모든 가능한 (x,y)의 집합 = S
dxdy=\int_{-1}^{1}\int_{x^2}^{1}cx^2ydydx=\frac{4}{21}c=1,\;c=\frac{21}{4} "$\int\int_S f(x,y)dxdy=\int_{-1}^{1}\int_{x^2}^{1}cx^2ydydx=\frac{4}{21}c=1,\;c=\frac{21}{4}$")
Let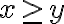
를 만족하는 S의 부분집합 = A
=\int\int_A f(x,y)dxdy=\int_0^1\int_{x^2}^{x}\frac{21}{4}x^2ydydx=\frac{3}{10} "$P(X\ge Y)=\int\int_A f(x,y)dxdy=\int_0^1\int_{x^2}^{x}\frac{21}{4}x^2ydydx=\frac{3}{10}$")
Let