확률변수,random_variable가 여러 개(두 개 이상)일 때.
Sub:
Compare:
이름으로 보아 related:
Compare:
이름으로 보아 related:
결합누적분포함수,joint_cumulative_distribution_function,joint_CDF
결합확률밀도함수,joint_probability_density_function,joint_PDF
결합확률질량함수,joint_probability_mass_function,joint_PMF - 여기에 정의 있음
결합확률분포의 엔트로피,entropy: 정보및부호화이론,information_and_coding_theory의 HW #4 요약 참조.결합확률밀도함수,joint_probability_density_function,joint_PDF
결합확률질량함수,joint_probability_mass_function,joint_PMF - 여기에 정의 있음
아래 셋 비교
Joint CDF(결합누적분포함수,joint_cumulative_distribution_function,joint_CDF):
=P(X\le x,Y\le y))
Joint PDF(결합확률밀도함수,joint_probability_density_function,joint_PDF):
=\frac{F_{X,Y}(x,y)}{dxdy}) ...분자 앞부분에
...분자 앞부분에 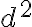 이 빠진 거 아닌지? chk; 그리고 보통 d 대신 ∂을 쓰던데 이것도 옳은지 chk
이 빠진 거 아닌지? chk; 그리고 보통 d 대신 ∂을 쓰던데 이것도 옳은지 chk
Joint PMF(결합확률질량함수,joint_probability_mass_function,joint_PMF):
=P(X=x,Y=y))
tmp from http://bigdata.dongguk.ac.kr/lectures/med_stat/_book/확률변수분포.html#확률변수의-결합분포와-독립
// ㄷㄱㄱ Week 9-1 p5
Joint PMF and PDF
결합 pmf와 pdf의 관계에 대한 요약표.
Joint PMF and PDF
결합 pmf와 pdf의 관계에 대한 요약표.
| Discrete RVs | Continuous RVs | ||
| joint | joint pmf | joint pdf | 이산형은 그냥 연속형은 |
| marginal | marginal pmf | marginal pdf | x의 marginal pdf를 얻으려면 y에 대해 적분, y의 marginal pdf를 얻으려면 x에 대해 적분. |
| joint cdf | joint pmf/joint pdf를 가지고 cdf를 만들기? chk 좌표평면에서 ┐모양을 생각 (꺾어지는 점이 x,y 이고 그 왼쪽 아래 면적을 생각) | ||
| 오른쪽은 cdf를 미분해서 joint pdf 만들기? chk | |||
| x,y가 A라는 특정 영역에 속할 확률? | pmf에선 A에 속하는 모든 x, y 지점의 pmf 값을 더하면 되고 연속변수의 경우 pdf를 영역에 대해 적분하면 됨 |
Twins:
 Joint_probability_distribution
Joint_probability_distribution
 결합분포 (결합확률분포)
결합분포 (결합확률분포)
https://everything2.com/title/Joint Probability Distribution
이거 여기?
![[https]](/123/imgs/https.png) 수학백과: 결합분포함수
수학백과: 결합분포함수
https://everything2.com/title/Joint Probability Distribution
![[https]](/123/imgs/https.png) 수학백과: 결합분포함수
수학백과: 결합분포함수
