기호: 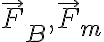
단위: 힘이므로 N (newton)
대전입자가 자기장 를 지날 때, 입자에 작용하는 자기력은
를 지날 때, 입자에 작용하는 자기력은
)
방향:
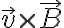 를 오른손 법칙으로 방향을 구한 다음
를 오른손 법칙으로 방향을 구한 다음 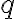 의 부호로 같은 방향인지 반대 방향인지를 결정
의 부호로 같은 방향인지 반대 방향인지를 결정
크기:
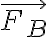 의 크기는
의 크기는 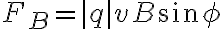
(φ는 v와 B 사이의 각도)
대전입자가 자기장
(φ는 v와 B 사이의 각도)
2. Force between two wires ¶
무한히 긴 두 도선이 각각 전류 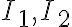 가 흐르고 거리
가 흐르고 거리 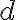 만큼 떨어져 있으면,
만큼 떨어져 있으면,
전류 방향이 같으면 서로 미는 힘이,
전류 방향이 반대면 서로 당기는 힘이 존재하며 그 자기력의 magnitude는 (in free space)
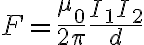
where
QQQ 왜 위랑 반대인가!?!?
전류 방향이 같으면 서로 미는 힘이,
전류 방향이 반대면 서로 당기는 힘이 존재하며 그 자기력의 magnitude는 (in free space)
QQQ 왜 위랑 반대인가!?!?
3. from Khan Academy ¶
자기장 B에서 속도 v로 움직이는 전하 q가 받는 힘은
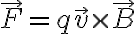
전류 I가 길이 L인 도선에 속도 v로 시간 t동안 흐른다면, (속도)=(거리)/(시간)이므로
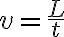
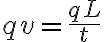
and since current is the amount of charge flowing per second, (q/t=I)

and therefore

4. 어떤 정리에 보면.. ¶

일정한 외부 자기장  속에 전류
속에 전류  가 흐르는 단면적
가 흐르는 단면적  , 길이
, 길이  인 도선의 한 부분을 생각.
인 도선의 한 부분을 생각.
전하 유동속도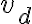 라면, 전하
라면, 전하 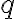 에 작용하는 자기력은
에 작용하는 자기력은
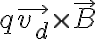
단위 부피당 전하의 수를  이라 할 때, 길이
이라 할 때, 길이  인 도선의 부피는
인 도선의 부피는 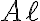 , 전하의 수는
, 전하의 수는 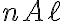
길이가 인 도선에 작용하는 전체 자기력은
인 도선에 작용하는 전체 자기력은
nA\ell)
도선의 전류는 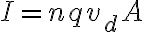 이므로,
이므로,
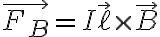
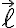 의 방향은 전류의 방향이며, 크기는 도선의 길이와 같음
의 방향은 전류의 방향이며, 크기는 도선의 길이와 같음
전하 유동속도
길이가
mv to somewhere?{
종류가 다른 극(N극과 S극) 사이에는 인력이 작용
같은 종류의 극(N극과 N극, S극과 S극) 사이에는 척력이 작용
}
종류가 다른 극(N극과 S극) 사이에는 인력이 작용
같은 종류의 극(N극과 N극, S극과 S극) 사이에는 척력이 작용
}
5. 자기장 속에서 움직이는 전하에 의한 자기력 ¶
(θ는 전류의 방향과 자기장의 사잇각)
그...상황..(TODO) 에서는 원운동을 하게 되는데
그 반지름 r....을 구하는 법은
원운동,circular_motion의 구심력,centripetal_force이 자기력과 같으므로
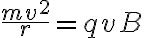
따라서
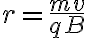
이 원리를 질량분석기(mass spectrometer) (Refer to 질량분석(mass spectrometry))가 이용함
그 반지름 r....을 구하는 법은
원운동,circular_motion의 구심력,centripetal_force이 자기력과 같으므로
사이클로트론도?
6. 전하의 등속원운동 및 사이클로트론 관련 ¶
균일한 자기장 B에서 전하 q가 등속원운동,uniform_circular_motion(curr. see 원운동,circular_motion)을 하면

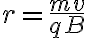
s=vt에서 t=s/v이므로 한 바퀴 도는 시간(주기,period)는
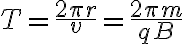
따라서 T는 전하의 속도 v나 원의 반지름 r에 무관. 이것을 사이클로트론 주기라고 하며, 사이클로트론 진동수는
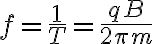
위에서 q와 m의 비가 같은 입자들은 동일한 자기장에서 주기가 같다는 것을 알 수 있음. q/m은 입자의 비전하,specific_charge라고 함.
7. 전류가 흐르는 도선에 작용하는 자기력 ¶
tmp; 송종현
{
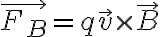
{
길이 L인 도선에, 전류가 i로 흐르고(즉 전자가 유동속도 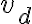 로 i의 반대방향으로 흐르고) 길이 L을 지나는 데 걸리는 시간이 t일 때
로 i의 반대방향으로 흐르고) 길이 L을 지나는 데 걸리는 시간이 t일 때
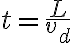 (s=vt이므로 t=s/v) 이고
(s=vt이므로 t=s/v) 이고 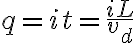 임.
임.
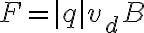
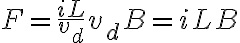
일반적으로, 길이 L이고 전류 i가 흐르는 도선이 받는 자기력은
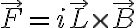
from http://www.kocw.net/home/search/kemView.do?kemId=1076465 자기장-2 31m
}
}
길이 ℓ 이고 단면적 A 인 도선이 자기장 B 안에 있고, 안에 전하(q)가 속도 v로 이동중.
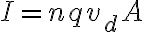
로 표기할 수 있는데 위에 적용하면
)
이것은 길이 ℓ만큼에 작용하는 힘이다.
(여기서 좀 살펴보니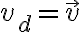 라는 가정 들어갔음....)
라는 가정 들어갔음....)
Magnitude는 물론
한 전하가 받는 힘은 
부피는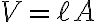
전하밀도(부피밀도)는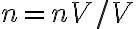 (=전하수/부피)
(=전하수/부피)
전하수는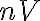
모든 전하가 받는 힘은nA\ell) (=전선이 받는 힘)
(=전선이 받는 힘) )
전류,electric_current는부피는
전하밀도(부피밀도)는
전하수는
모든 전하가 받는 힘은
(여기서 좀 살펴보니
Magnitude는 물론
Compare: 전기력,electric_force


![[http]](/123/imgs/http.png)