기호: μ, 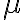
단위: N/A2, H/m
단위: N/A2, H/m
자기장은 물질(material) 안에서 증가 혹은 감소하는데, ?? cHK
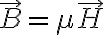
i.e.
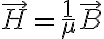
μ = B/H
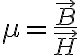 ...여기 이렇게 표기해도 되는지.. 벡터장을 ie 벡터기호를 abs 기호로 둘러싸야 하나?
...여기 이렇게 표기해도 되는지.. 벡터장을 ie 벡터기호를 abs 기호로 둘러싸야 하나?
자기장,magnetic_field에서, 자속밀도,magnetic_flux_density(B)와 자기장세기,magnetic_field_intensity(H)의 비율2. 상대투자율 µr ¶
상대 투자율(relative (magnetic) permeability), 비투자율
기호: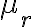
기호:
물질의 투자율과 진공의 투자율 비.
일반적으로 비자성체의 경우 1에 가까운 값을, 자성체의 경우 1보다 아주 큰 값을 갖는다.
일반적으로 비자성체의 경우 1에 가까운 값을, 자성체의 경우 1보다 아주 큰 값을 갖는다.
µr = µ / µ0
µ = µr µ0
µ = µr µ0
fork to 상대투자율,relative_permeability
nonmagnetic한 경우,
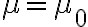
ferromagnetic material의 경우, 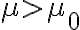 이며
이며
CHK
{
상대투자율이 높을수록 자석,magnet에 유도되기 쉽다. 즉 강자성체일수록 투자율이 높다. CHK
CHK
{
상대투자율이 높을수록 자석,magnet에 유도되기 쉽다. 즉 강자성체일수록 투자율이 높다. CHK
| 나무 | 1.00000043 |
| 알루미늄 | 1.000022 |
| 코발트 | 250 |
| 니켈 | 600 |
| 철 | 200,000 |
3. 참조 ¶
자기 감수율(magnetic susceptibility) χm = 자화율,magnetic_susceptibility
AKA: 자기 투과율, 자기투자율, magnetic permeability


![[https]](/123/imgs/https.png)