값: 2.7182818284…
오일러의 정의:
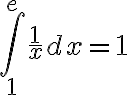
 is the number such that
is the number such that
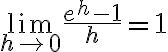
(Stewart)
명목 이자율 100%로 무한히 자주 복리 계산을 하는 대출에 대한 유효 이자율(연간 성장률)은 얼마인가? 답은 e이다. 만약 오늘 1000달러를 빌리면, 1년 후에는 2718.28달러를 빚진다.
(Ivan Savov p475)
(Ivan Savov p475)
AKA: base of natural logarithm, Napier's constant, Euler's number (다만 오일러 상수 AKA 오일러-마스케로니 상수 Euler–Mascheroni constant γ = 0.57721… 는 다른 수이다.)


![[http]](/123/imgs/http.png)