Difference between r1.39 and the current
@@ -8,6 +8,11 @@
TI-Nspire:
nCr(n,r)
= Simple Example =
이런 건 공식에 대입하지 않는 게 더 계산하기 편한 경우.
,,5,,C,,2,, = ,,5,,P,,2,, / 2! = 5×4 / 2×1 = 10
,,7,,C,,3,, = ,,7,,P,,3,, / 3! = 7×6×5 / 3×2×1 = 35
= 성질 =
'아무것도 선택하지 않은 경우'는 하나의 경우. (조합의 수가 1)
@@ -20,6 +25,8 @@
$_n\mathrm{C}_r=\,_n\mathrm{C}_{n-r}$i.e.
$\binom{n}{k}=\binom{n}{n-k}$
rel. [[파스칼_삼각형,Pascal_triangle]]
$C(n,r)\times r!=P(n,r)$
@@ -27,6 +34,10 @@
$C(n,r)=\frac{P(n,r)}{r!}$순열과 달리 '''조합'''에선 배열 순서가 상관없으므로, (순열의 수)를 (배열하는 경우의 수)로 나누어 주면 ('''조합의 수''').
MKLINK
[[배열,arrangement]]?
[[순서,order]]
Compare: [[순열,permutation]]
@@ -51,7 +62,7 @@
== 중복조합의 여러 가지 표기법 ==
${}_n\mathrm{H}_{\,r}$ 기호는 한국에서만 쓰나?
${}_n\mathrm{H}_{\,r}$ 기호는 한국 or 한국+일본에서만 쓰나? 영어권 국가에서 저걸 쓰는 걸 한번도 못 봤다.
$(({n\\r}))$$\langle{n\\r}\rangle$
@@ -71,7 +82,18 @@
비슷: [[이항계수,binomial_coefficient]]이름이 관련:
영단어 combination은 선형대수에선 [[선형결합,linear_combination]]
영단어 combination은 선형대수에선 조합이 아닌 결합으로 번역 - [[결합,combination]] - [[선형결합,linear_combination]] etc.
[[결합,combination]] [[RR:결합,combination]]
{
[[볼록결합,convex_combination]]
[[WtEn:convex_combination]]
[[유클리드_공간,Euclidean_space]]의 [[벡터,vector]]들의 [[선형결합,linear_combination]]인데 계수들이 비음수이고 모두 합해서 1인 경우.
[[아핀결합,affine_combination]]
[[WtEn:affine_combination]]
}
Related:
[[조합론,combinatorics]]
@@ -83,5 +105,4 @@
https://www.encyclopediaofmath.org/index.php/Combinationhttps://artofproblemsolving.com/wiki/index.php/Combination
표기: 
서로 다른 
개에서 
개를 택하는 조합의 수는
!}\qquad\qquad(0\le r \le n) "${}_{n}\mathrm{C}_{r}=\frac{{}_{n}\mathrm{P}_{r}}{r!}=\frac{n!}{r!(n-r)!}\qquad\qquad(0\le r \le n)$")
TI-Nspire:
nCr(n,r)
Simple Example ¶
이런 건 공식에 대입하지 않는 게 더 계산하기 편한 경우.
5C2 = 5P2 / 2! = 5×4 / 2×1 = 10
7C3 = 7P3 / 3! = 7×6×5 / 3×2×1 = 35
5C2 = 5P2 / 2! = 5×4 / 2×1 = 10
7C3 = 7P3 / 3! = 7×6×5 / 3×2×1 = 35
성질 ¶
'아무것도 선택하지 않은 경우'는 하나의 경우. (조합의 수가 1)
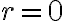일 때,
!}=1 "${}_n\mathrm{C}_0=\frac{n!}{0!(n-0)!}=1$")
'모두 선택한 경우' 역시 하나의 경우. (조합의 수가 1)
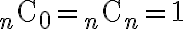
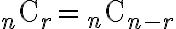
i.e.
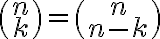
rel. 파스칼_삼각형,Pascal_triangle
i.e.
rel. 파스칼_삼각형,Pascal_triangle
순열(permutation)과의 관계 ¶
표기 ¶
TeX의 조합 표기법은
x \choose y =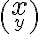
\binom{x}{y} =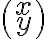
x \choose y =
\binom{x}{y} =
이고, 정식 방법은 아니지만
\left({x \atop y}\right) = "$\left({x \atop y}\right)$")
(이상 세 개의 렌더링이 미묘하게 다르다)
\begin{pmatrix}x\\y\end{pmatrix} =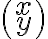
\left({x \atop y}\right) =
\begin{pmatrix}x\\y\end{pmatrix} =
Prg Lang Impl - Programming Language Implementations ¶
Up: 순열과_조합_비교
이름이 관련:
영단어 combination은 선형대수에선 조합이 아닌 결합으로 번역 - 결합,combination - 선형결합,linear_combination etc.
결합,combination
결합,combination
{
영단어 combination은 선형대수에선 조합이 아닌 결합으로 번역 - 결합,combination - 선형결합,linear_combination etc.
결합,combination
결합,combination{
