중간값정리,사이값정리,intermediate_value_theorem,IVT

중간값정리,사이값정리,intermediate_value_theorem,IVT (rev. 1.16)
$f$ 가 $[a,b]$ 에서 정의된 함수이며 $W$ 는 $f(a)$ 와 $f(b)$ 사이의 값이라고 하자.
$f$ 가 $[a,b]$ 에서 연속일 때,
$f(c)=W$ 인 $c$ 가 $a$ 와 $b$ 사이에 존재한다.
함수 $f(x)$ 가 폐구간 $[a,\,b]$ 에서 연속이고 $f(a)\neq f(b)$ 일 때,
$f(a)$ 와 $f(b)$ 사이의 임의의 실수 $k$ 에 대하여
$f(c)=k$
인 c가 a와 b 사이에 적어도 하나 존재한다.
Let $f:[a,b]\mapsto\mathbb{R}$ be a continuous function.
Then for all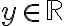 $y\in\mathbb{R}$ between $f(a)$ and $f(b)$
there exists a value $x\in[a,b]$ such that $f(x)=y$ .
Suppose $f$ is continuous on a closed interval $[a,b]$ .
$\forall k \textrm{ between } f(a) \textrm{ and } f(b)$
$\exists c \in [a,b] \,\textrm{ such that }\, f(c)=k$


[edit]

중간값 성질 intermediate value property

$f$ 는 폐구간 $[a,b]$ 상에서 연속함수이고, $y_0$ 는 $f(a)$ 와 $f(b)$ 사이의 임의의 수이면,
$y_0=f(c)$ 를 만족하는 수 $c\in[a,b]$ 가 존재한다.

[edit]

tmp links

[edit]

기타

증명: 볼차노의 1817년 논문
엄밀한 증명: Cauchy, 1821년

비슷한 게 다르부_정리,Darboux_theorem
{
Darboux's theorem

// 수학백과 summary
미분가능한 실함수의 도함수는 사잇값 성질을 가진다,
ie
미분가능 함수의 도함수는 연속함수가 아니더라도 사잇값 성질을 가진다는 것

사잇값 성질을 만족하는 함수를 다르부 함수(Darboux function)라고 하기도