Difference between r1.5 and the current
@@ -1,8 +1,12 @@
적분 식
$\int f(x)dx$에서
$x=g(t)$
로 놓으면, $g(t)$ 가 미분가능할 때
에서 $x=g(t)$ 로 놓으면, $g(t)$ 가 미분가능할 때
$\int f(x)dx=\int f(g(t))g'(t)dt$= 치환적분 =
(정리) $u=g(x)$ 를 미분가능한 함수라 하고 그 치역을 $I,$ $f$ 를 $I$ 위에서 연속이라고 하면 다음이 성립.
$\int f(g(x))g'(x)dx=\int f(u)du$
(Thomas 13e ko p277)
= 정적분의 치환적분법 =
구간 $(a,b)$ 에서 $g'$ 이 연속이고,
@@ -12,32 +16,18 @@
----
##고딩교과서에서.
미분가능한 함수 $t=g(x)$ 의 도함수 $g'(c)$ 가 구간 $[a,b]$ 에서 연속이고,
미분가능한 함수 $t=g(x)$ 의 도함수 $g'(x)$ 가 구간 $[a,b]$ 에서 연속이고,
$g(a)=\alpha,\,g(b)=\beta$ 에 대해 함수 $f(t)$ 가 $\alpha,\beta$ 를 양 끝으로 하는 닫힌 구간에서 연속일 때$\int_a^b f(g(x))g'(x)dx=\int_{\alpha}^{\beta}f(t)dt$
----
미분의 [[연쇄법칙,chain_rule]]에 대응.
'''치환적분'''은 연쇄법칙을 거꾸로 실행한 것.
(Thomas 13e ko p275밑)
일변수 함수는 치환을 쓴 치환적분 ... 다변수 함수는 변환을 쓴 [[야코비안,Jacobian]]? CHK
----
Up: [[치환,substitution]] [[적분,integration]]
적분 식
dx)
에서 ) 로 놓으면,
로 놓으면, ) 가 미분가능할 때
가 미분가능할 때
dx=\int f(g(t))g%27(t)dt)
정적분의 치환적분법 ¶
구간 ) 에서
에서 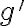 이 연속이고,
이 연속이고,
 가
가 ) 의 치역에서 연속이면 다음 식이 성립:
의 치역에서 연속이면 다음 식이 성립:
)g%27(x)dx=\int_{g(a)}^{g(b)}f(u)du)
미분가능한 함수 ) 의 도함수
의 도함수 ) 가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속이고,
에서 연속이고,
=\alpha,\,g(b)=\beta) 에 대해 함수
에 대해 함수 ) 가
가 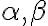 를 양 끝으로 하는 닫힌 구간에서 연속일 때
를 양 끝으로 하는 닫힌 구간에서 연속일 때
)g%27(x)dx=\int_{\alpha}^{\beta}f(t)dt)
미분의 연쇄법칙,chain_rule에 대응.
치환적분은 연쇄법칙을 거꾸로 실행한 것.
(Thomas 13e ko p275밑)
(Thomas 13e ko p275밑)
일변수 함수는 치환을 쓴 치환적분 ... 다변수 함수는 변환을 쓴 야코비안,Jacobian? CHK

