기호/표기: 복소수 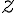 의 켤레복소수는
의 켤레복소수는
 (주로 수학에서 쓰임)
(주로 수학에서 쓰임)
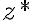 (주로 물리와 공학에서 쓰임)
(주로 물리와 공학에서 쓰임)
복소수
)
의 켤레복소수는

즉 허수부의 부호,sign를 바꾼(반전시키는) 것.
i.e.
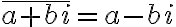
켤레복소수는 원래 복소수를 복소평면,complex_plane의 실수축에 대칭한 곳의 복소수.
i.e.
성질 ¶
복소수 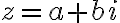 일 때,
일 때,
실계수 다항식 ) 에서
에서 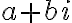 가
가 =0) 의 해이면 켤레
의 해이면 켤레 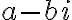 도 해가 됨
도 해가 됨
TBW:
conjugate_matrix
conjugate_matrix
특히 notation 확실히 정리
Twins:
 켤레_복소수
켤레_복소수
https://mathworld.wolfram.com/ComplexConjugate.html
https://everything2.com/title/complex conjugate
https://planetmath.org/complexconjugate
https://mathworld.wolfram.com/ComplexConjugate.html
https://everything2.com/title/complex conjugate
https://planetmath.org/complexconjugate
Semi-twins:
https://en.citizendium.org/wiki/Complex_conjugation - 아마 complex_conjugate 를 구하는 행동(연산,operation)이 - 즉 imaginary_part 의 부호,sign를 reverse하는 행동이 - complex_conjugation ? CZ says so.
https://en.citizendium.org/wiki/Complex_conjugation - 아마 complex_conjugate 를 구하는 행동(연산,operation)이 - 즉 imaginary_part 의 부호,sign를 reverse하는 행동이 - complex_conjugation ? CZ says so.
AKA conjugate complex number, 공액복소수, 복소켤레, 복소공액

