Difference between r1.12 and the current
@@ -1,4 +1,8 @@
$(a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2)\ge(a_1b_1+a_2b_2+\cdots+a_nb_n)^2$----
임의의 실수 $x_1,x_2,\cdots,x_k$ 와 $y_1,y_2,\cdots,y_k$ 에 대해 다음이 성립.
$(x_1y_1+x_2y_2+\cdots+x_ky_k)^2\le(x_1^2+x_2^2+\cdots+x_k^2)(y_1^2+y_2^2+\cdots+y_k^2)$
## from 수학백과 절대부등식
----$a_i,b_i\in\mathbb{R}$
$\left(\sum_{i=1}^{n}a_i^2\right)^{\frac12} \left(\sum_{i=1}^{n}b_i^2\right)^{\frac12} \ge \left| \sum_{i=1}^{n}a_ib_i \right|$
@@ -6,15 +10,37 @@
[[벡터,vector]]로 나타내면$|\vec{x}| |\vec{y}| \ge |\vec{x} \cdot \vec{y}| $
등식이 될 필요충분조건은 두 벡터가 평행? CHK
----
$\mathbb{R}^n$ 의 임의의 벡터 $\vec{x},\vec{y}$ 에 대해 다음이 성립.$|\vec{x}\cdot\vec{y}|\le ||x||\, ||y||$
단, 등호는 $\vec{x},\vec{y}$ 중 하나가 다른 것의 실수배일 때만 성립.
## from BigBook-LinearAlgebra-2015 정리 1.2-2
----
정리)
$|\vec{a}\cdot\vec{b}| \le |\vec{a}| \cdot |\vec{b}|$
Pf.
$\vec{a}=(a_1,\cdots,a_n)$
$\vec{b}=(b_1,\cdots,b_n)$
$(a_1-tb_1)^2+(a_2-tb_2)^2+\cdots+(a_n+tb_n)^2 \ge 0 \quad \forall t$
$(b_1^2 + \cdots + b_n^2)t^2 - 2(a_1b_1 + \cdots + a_nb_n)t + (a_1^2 + \cdots + a_n^2) \ge 0 \quad \forall t$
[[판별식,discriminant]] $D/4=(a_1b_1+\cdots+a_nb_n)^2-(a_1^2+\cdots+a_n^2)(b_1^2+\cdots+b_n^2)\le 0$
$(\vec{a}\cdot\vec{b})^2 \le |\vec{a}|^2 \cdot |\vec{b}|^2$
$|\vec{a}\cdot\vec{b}| \le |\vec{a}| \cdot |\vec{b}|$
(저기서 얻을 수 있는) 결론:
$-1\le \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}\le 1$
그리고 $\theta\in[0,\pi]$ 에 대해,
$\exists!\theta$ such that $\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}=\cos\theta$
$\vec{a}\cdot\vec{b}=|\vec{a}| |\vec{b}| \cos\theta$
즉 임의의 n차원 공간에서 [[내적,inner_product]]을 가지고 두 [[벡터,vector]]사이의 [[각,angle]]을 정의할 수 있다.
순수하게 대수적인 것에서 기하적인 것을 뽑아낸 예.
from 김도형 http://www.kocw.net/home/search/kemView.do?kemId=1141060 5. 35m
----
$|\vec{A}\cdot\vec{B}|^2\le(\vec{A}\cdot\vec{A})(\vec{B}\cdot\vec{B})$$|\vec{A}\cdot\vec{B}|\le ||\vec{A}|| \cdot ||\vec{B}|| $
@@ -25,13 +51,38 @@
$=t^2(A\cdot A)+2t(A\cdot B)+B\cdot B$$A\cdot A=0$ 인 경우, 부등식이 성립
$A\cdot A\ne0$ 인 경우, t에 대한 2차식인데 이게 항상 0 이상이므로, 판별식을 생각하면 부등식이 성립
from 계승혁, 인문사회계를 위한 수학 2-03-1
http://snui.snu.ac.kr/ocw/index.php?mode=view&id=1180
$\vec{F},\vec{G}$ 가 둘 다 영벡터가 아니면
$\cos\theta=\frac{\vec{F}\cdot\vec{G}}{||\vec{F}|| \, ||\vec{G}||}$
그런데 $\forall\theta,\,|\cos\theta|\le 1$ 이므로 이것은 Cauchy-Schwarz 부등식을 암시한다.
$|\vec{F}\cdot|\vec{G}|\le ||\vec{F}||\, ||\vec{G}||$
$\cos(\theta)=\frac{\vec{F}\cdot\vec{G}}{||\vec{F}|| \, ||\vec{G}||}$
그런데 $\forall\theta,\,|\cos(\theta)|\le 1$ 이므로 이것은 Cauchy-Schwarz 부등식을 암시한다.
$|\vec{F}\cdot\vec{G}|\le ||\vec{F}||\, ||\vec{G}||$
(O'Neil AEM (6.1))이 부등식은 [[함수공간,function_space]]에서 [[함수,function]]에 대해서도 성립. 수식은 [[함수공간,function_space#s-1]] 밑부분 참조. (문자열 찾기로 cauchy-sch 검색)
----
Twins:
[[https://namu.wiki/w/%EC%BD%94%EC%8B%9C-%EC%8A%88%EB%B0%94%EB%A5%B4%EC%B8%A0%20%EB%B6%80%EB%93%B1%EC%8B%9D Namu: 코시-슈바르츠 부등식]]
[[https://terms.naver.com/entry.naver?docId=3405363&cid=47324&categoryId=47324 수학백과: 코시-슈바르츠 부등식]]
[[WpKo:코시-슈바르츠_부등식]]
[[WpEn:Cauchy–Schwarz_inequality]]
https://encyclopediaofmath.org/wiki/Cauchy_Schwarz_inequality
https://encyclopediaofmath.org/wiki/Bunyakovskii_inequality
https://mathworld.wolfram.com/CauchysInequality.html
https://mathworld.wolfram.com/SchwarzsInequality.html
https://everything2.com/title/Cauchy-Schwarz+inequality
https://www.probabilitycourse.com/chapter6/6_2_4_cauchy_schwarz.php
Semi-twins:
[[https://terms.naver.com/entry.naver?docId=4125197&cid=60207&categoryId=60207 수학백과: 내적공간]] section 3.코시-슈바르츠 부등식
''그러고보니 MKLINK: [[내적공간,inner_product_space]] [[내적,inner_product]]''
----
Compare: [[삼각부등식,triangle_inequality]]
Up: [[부등식,inequality]]
임의의 실수 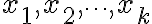 와
와 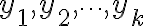 에 대해 다음이 성립.
에 대해 다음이 성립.
^2\le(x_1^2+x_2^2+\cdots+x_k^2)(y_1^2+y_2^2+\cdots+y_k^2))
정리)
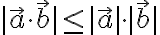
(저기서 얻을 수 있는) 결론:
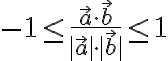
그리고 ![$\theta\in[0,\pi]$ $\theta\in[0,\pi]$](/123/cgi-bin/mimetex.cgi?\Large \theta\in[0,\pi]) 에 대해,
에 대해,
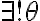 such that
such that 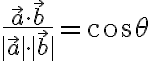
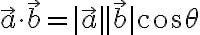
from 김도형 http://www.kocw.net/home/search/kemView.do?kemId=1141060 5. 35m
pf.
\cdot(tA+B))
)+B\cdot(tA+B))
+A\cdot B)+B\cdot(tA)+B\cdot B)
+2t(A\cdot B)+B\cdot B)
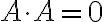 인 경우, 부등식이 성립
인 경우, 부등식이 성립
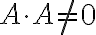 인 경우, t에 대한 2차식인데 이게 항상 0 이상이므로, 판별식을 생각하면 부등식이 성립
인 경우, t에 대한 2차식인데 이게 항상 0 이상이므로, 판별식을 생각하면 부등식이 성립
이 부등식은 함수공간,function_space에서 함수,function에 대해서도 성립. 수식은 함수공간,function_space#s-1 밑부분 참조. (문자열 찾기로 cauchy-sch 검색)
Twins:
![[https]](/123/imgs/https.png) Namu: 코시-슈바르츠 부등식
Namu: 코시-슈바르츠 부등식
![[https]](/123/imgs/https.png) 수학백과: 코시-슈바르츠 부등식
수학백과: 코시-슈바르츠 부등식
 코시-슈바르츠_부등식
코시-슈바르츠_부등식
 Cauchy–Schwarz_inequality
Cauchy–Schwarz_inequality
https://encyclopediaofmath.org/wiki/Cauchy_Schwarz_inequality
https://encyclopediaofmath.org/wiki/Bunyakovskii_inequality
https://mathworld.wolfram.com/CauchysInequality.html
https://mathworld.wolfram.com/SchwarzsInequality.html
https://everything2.com/title/Cauchy-Schwarz inequality
https://www.probabilitycourse.com/chapter6/6_2_4_cauchy_schwarz.php
![[https]](/123/imgs/https.png) Namu: 코시-슈바르츠 부등식
Namu: 코시-슈바르츠 부등식![[https]](/123/imgs/https.png) 수학백과: 코시-슈바르츠 부등식
수학백과: 코시-슈바르츠 부등식https://encyclopediaofmath.org/wiki/Cauchy_Schwarz_inequality
https://encyclopediaofmath.org/wiki/Bunyakovskii_inequality
https://mathworld.wolfram.com/CauchysInequality.html
https://mathworld.wolfram.com/SchwarzsInequality.html
https://everything2.com/title/Cauchy-Schwarz inequality
https://www.probabilitycourse.com/chapter6/6_2_4_cauchy_schwarz.php

