파수, 파동수, wave number, wavenumber
단위길이당 파의 수 CHK
단위길이당 변화하는 위상,phase의 크기.
한 파장,wavelength 만큼 지나면 ( 같은 패턴이 반복 ) i.e. (
만큼 지나면 ( 같은 패턴이 반복 ) i.e. (  만큼 위상 차이가 생김 ). 따라서 파수는
만큼 위상 차이가 생김 ). 따라서 파수는
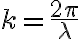
(물리학백과 파수)
한 파장,wavelength
높은 차원으로 확장하면 위치벡터,position_vector 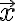 와 파수벡터(
와 파수벡터(  wavenumber vector하면
wavenumber vector하면  Wave_vector가 제시되는데 같은거? chk. wavenumber_vector == wave_vector ?
Wave_vector가 제시되는데 같은거? chk. wavenumber_vector == wave_vector ?  파수벡터 =
파수벡터 =  파동벡터 ? chk. -> wavenumber는 wavevector의 magnitude임. 다시 말해
파동벡터 ? chk. -> wavenumber는 wavevector의 magnitude임. 다시 말해  )
) 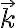 를 생각할 수 있고,
를 생각할 수 있고,
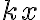 를
를 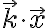
로 바꿀 수 있다.
(![[https]](/123/imgs/https.png) 물리학백과: 사인파 # 수학적 기술)
물리학백과: 사인파 # 수학적 기술)
(
![[https]](/123/imgs/https.png) 물리학백과: 사인파 # 수학적 기술)
물리학백과: 사인파 # 수학적 기술)비교
| 파수,wavenumber | 각파동수(angular wave number) k | 파장,wavelength(λ)과 reciprocal | |
| 각진동수,angular_frequency | 각진동수(angular frequency) ω | 주기,period(T)와 reciprocal |
오른쪽(+)으로 진행하는 1차원 sin형 파동함수,wave_function는
=f_m\sin(kx-\omega t))
여기서
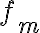 : 진폭,amplitude
: 진폭,amplitude
 : 각파동수(angular wave number) = 파수(wavenumber) :
: 각파동수(angular wave number) = 파수(wavenumber) :  안에 공간적 주기
안에 공간적 주기  가 몇 번 들어있는지를 알려주는 요소
가 몇 번 들어있는지를 알려주는 요소
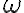 : 각진동수(angular frequency) :
: 각진동수(angular frequency) :  안에 시간적 주기
안에 시간적 주기 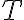 가 몇 번 반복되는지를 알려주는 요소
가 몇 번 반복되는지를 알려주는 요소
이를 이용해 위 식을 다시 쓰면
=f_m\sin 2\pi\left( \frac{x}{\lambda}-\frac{t}{T} \right))
(From https://m.blog.naver.com/spin898/221155896887)
다른 책은 단위 rad/s 라는데 뭐가 맞는 거?
조화파의 방정식을 다음과 같이 쓸 수 있다
=A\cos(\omega t-kx)) (wave moving along
(wave moving along 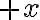 direction)
direction)
=A\cos(\omega t+kx)) (wave moving along
(wave moving along 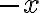 direction)
direction)
Phase constant가 아닌 phase에 대해서는 see 위상,phase

