파동함수,wave_function

AKA wavefunction

파동량을 공간, 시간에 대한 함수로서 기술할 수 있다. complex-valued_function임.

기호 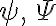$\psi,\,\Psi$




(슈뢰딩거_방정식,Schroedinger_equation 등 파동방정식의 해인) "파동함수를 제곱,square하면 입자,particle의 존재확률이지만, 파동함수 그 자체의 값은 의미를 알 수 없음" chk; from https://blog.naver.com/cwhaha/70074757638

//물백
양자역학,quantum_mechanics에서 양자계의 상태를 나타내는 복소함수. 상태함수,state_function라고도 한다. 1. 물리에서? 2. 그럼 파동함수는 상태함수의 일종?
물질의 파동성 때문에 계(양자계?)의 시간에 따른 변화는 파동의 진행(propagation? WpEn:Wave_propagation 이거?)과 비슷하며 슈뢰딩거_방정식,Schroedinger_equation으로 기술된다.
QM의 표준해석인 통계적 해석 즉 코펜하겐_해석,Copenhagen_interpretation에 따르면, 파동함수의 절대값 제곱은 물질이 입자성을 가지고 어떤 위치에서 발견될 확률밀도(rel. 확률밀도함수,probability_density_function,PDF)를 알려준다.
....(2. 복소함수, 중첩) 파동함수는 복소함수인데 복소함수는 크기magnitude? 뿐만 아니라 위상,phase을 가지고 있으므로 파동의 중요한 성질인 간섭,interference을 잘 기술할 수 있다. 파동방정식,wave_equation은 선형방정식,linear_equation이므로 복소함수는 벡터,vector와 비슷한 성질을 많이 갖고 있다. 두 파동함수의 합 및 이를 일반화한 여러 파동함수의 선형결합,linear_combination으로 파동함수를 만들 수 있다. 복소함수의 선형결합은 위상차,phase_difference 때문에 상쇄되어 전체 함수의 크기가 작아질 수도 있다. 이러한 성질을 중첩,superposition이라고 한다. / 이러한 함수들의 집합은 수학에서 힐베르트_공간,Hilbert_space으로 잘 알려져 있다.
....(3. 통계적 해석)....
똑같은 양자계가 여러 개 있다고 가정하자. 이를 앙상블,ensemble이라 한다. ....



[edit]

1. from ktword 파동함수 ; chk

시간,time과 공간,space에 대해 - 항상?

[edit]

1.1. 공간만 고려한 파동함수의 표현

$\Psi(\vec{r})=A\cos(\vec{k}\cdot\vec{r})$ (또는 cos대신 sin)
$\Psi(\vec{r})=Ae^{j\vec{k}\cdot\vec{r}}$
공간에서 반복되는 것을 표현하면
$\Psi(\vec{r})=\Psi(\vec{r}+\lambda \frac{\vec{k}}{k})$

$\lambda$ : 파장,wavelength
$k$ : 파수,wavenumber
$\vec{k}/k$ : $\vec{k}$ 방향(???)의 단위벡터

[edit]

1.2. 시간도 고려해서, 진행하는 파로써 파동함수의 표현

길어서 생략. tbw.

[edit]

2. wave page에 있던거

{

Ψ2 = 확률밀도,probability_density
확률이 0이 되는 부분이 마디,node


  • 파동 함수 자체는 측정하거나 관찰 불가
  • 파동 함수의 절대값의 제곱은 특정 위치에서 입자를 발견할 확률 밀도를 알려줌, 이 값에 주변 부피를 곱하면 그 공간에서 입자를 발견한 확률


Ref:
http://physica.gsnu.ac.kr/phtml/wave/wave/represent/represent.html



오비탈,orbital과 같은 것?

}

[edit]

3. tmp 1


/* 1차원 파동함수 wave function을 fourier series로 분석 */

오른쪽(+)으로 진행하는 1-D sinusoidal wave function은 이렇게 표기:
$f(x,t)=f_m\sin(kx-\omega t)$
여기서
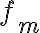$f_m$ : 진폭
$k$ : 각파동수 angular wave number (see 파수,wavenumber)
$2\pi$ 안에 공간주기 $\lambda$ (파장,wavelength) 가 몇 번 들어있는지를 알려줌.
$k=\frac{2\pi}{\lambda}$
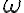$\omega$ : 각진동수 angular frequency (see 각진동수,angular_frequency)
$2\pi$ 안에 시간주기 $T$ (주기,period) 가 몇 번 반복되는지를 알려줌.
$\omega=\frac{2\pi}{T}$
(이상 두 개는 주기,period였음)
바로 위에 두 개 짧게 나온 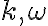$k,\omega$ 식으로 저 위에 wave function 식을 다시 쓰면
$f(x,t)=f_m \sin 2\pi \left( \frac{x}{\lambda} - \frac{t}{T} \right)$

푸리에_급수,Fourier_series는 기본적으로
1변수 함수에 대한 급수전개(멱급수,power_series 전개,expansion)이다. 따라서
2변수를 갖는 파동함수의 경우 둘 중 하나가 통제된(고정된) 함수를 기저함수,basis_function(curr 기저,basis)로 사용하게 된다. 따라서 주기가 각각 $\lambda,T$ 인 다음 두 함수를 쓴다.
$f_n(x)=\sin\left( \frac{2n\pi x}{\lambda} \right)$
$f_n(t)=\sin\left( \frac{2n\pi t}{T} \right)$
이걸 실제 파동함수 꼴로 바꿔주면
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left( a_n\cos\frac{2n\pi x}{\lambda} + b_n \sin \frac{2n\pi x}{\lambda} \right)$
$\begin{cases} \displaystyle a_n=\frac2{\lambda}\int_{-\lambda/2}^{+\lambda/2}f(x)\cdot \cos \frac{2n\pi x}{\lambda} dx\\ \displaystyle b_n=\frac2{\lambda}\int_{-\lambda/2}^{+\lambda/2}f(x)\cdot \sin \frac{2n\pi x}{\lambda} dx\end{cases}$

$\displaystyle f(t)=\frac{a_0}2+\sum_{n=1}^{\infty}\left( a_n \cos \frac{2n\pi t}{T} + b_n \sin \frac{2n\pi t}{T} \right)$
$\begin{cases}\displaystyle a_n=\frac2T \int_{-T/2}^{+T/2} f(t)\cdot \cos \frac{2n\pi t}{T} dt \\ \displaystyle a_n=\frac2T \int_{-T/2}^{+T/2} f(t)\cdot \sin \frac{2n\pi t}{T} dt \end{cases}$

[edit]

3.1. Fourier 급수 복소수 표현

$e^{i\pi}+1=0$
$e^{ikx}=\cos kx+i\sin kx$
$e^{-ikx}=\cos kx-i\sin kx$
여기서
$\cos kx=\frac{e^{ikx}+e^{-ikx}}{2}$
$\sin kx=\frac{e^{ikx}-e^{-ikx}}{2i}$
이고 이걸 써서 Fourier series에 기저함수로 쓰이는 삼각함수의 주기와 관련한 인자를 $\lambda,T$ 를 써서 다시 표기하면
$\cos\frac{2n\pi x}{\lambda}=\frac{e^{i \frac{2n\pi x}{\lambda}}+e^{-i \frac{2n\pi x}{\lambda}}}{2}$
$\sin\frac{2n\pi x}{\lambda}=\frac{e^{i \frac{2n\pi x}{\lambda}}-e^{-i \frac{2n\pi x}{\lambda}}}{2i}$
$(n=1,2,3,\ldots)$
이제 원래 Fourier series의 cos과 sin 항을 모두 지수함수로 바꿔 쓰면
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[a_n\cdot\left(\frac12\right)\cdot\left(e^{i\frac{2n\pi x}{\lambda}}+e^{-i\frac{2n\pi x}{\lambda}}\right)+b_n\cdot\left(\frac1{2i}\right)\cdot\left(e^{i\frac{2n\pi x}{\lambda}}-e^{-i \frac{2n\pi x}{\lambda}}\right)\right]$
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left [ \left(\frac{a_n}{2}+\frac{b_n}{2i}\right) e^{i \frac{2n\pi x}{\lambda}} + \left(\frac{a_n}{2}-\frac{b_n}{2i}\right) e^{-i \frac{2n\pi x}{\lambda}} \right]$
$a_n,b_n$ 이 포함된 ( ) 안의 항을 각각 $c_n,c_{-n}$ 으로 표기하면
$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[ c_ne^{i\frac{2n\pi x}{\lambda}} + c_{-n}e^{-i \frac{2n\pi x}{\lambda}}\right]$
$n=0$ 인 경우 $c_0$ 라 하고, 등등, 하여 간단히 하면
$f(x)=\sum_{n=-\infty}^{n=+\infty}c_ne^{i\frac{2n\pi x}{\lambda}}$
(복소수 형태의 Fourier series.) 이제 계수 $c_n$ 을 결정하려면? (중간 생략)
$c_n=\frac2{\lambda}\int_{-\lambda/2}^{+\lambda/2}f(x)\cdot e^{-i \frac{2n\pi x}{\lambda}}dx$

그리하여 최종정리하면
$f(x)=\frac{a_0}2+\sum_{n=1}^{\infty}\left( a_n\cos\frac{2n\pi x}{\lambda} + b_n\sin\frac{2n\pi x}{\lambda} \right) = \sum_{n=-\infty}^{\infty}c_n e^{i\frac{2n\pi x}{\lambda}}$
그리고
$a_n=\frac2{\lambda}\int_{-\lambda/2}^{\lambda/2} f(x) \cos \frac{2n\pi x}{\lambda} dx$
$b_n=\frac2{\lambda}\int_{-\lambda/2}^{\lambda/2} f(x) \sin \frac{2n\pi x}{\lambda} dx$
$c_n=\frac1{\lambda}\int_{-\lambda/2}^{\lambda/2} f(x) e^{-i \frac{2n\pi x}{\lambda}}dx$

간단히 하기 위해 주기가 $2\lambda,2T$ 인 함수를 고려하면 식의 2를 없앨 수 있다 (적분 상한 하한도 $\lambda$ 로 바뀜)
$f(x)=\frac{a_0}2+\sum_{n=1}^{\infty}\left( a_n\cos\frac{n\pi x}{\lambda} + b_n\sin\frac{n\pi x}{\lambda}\right)=\sum_{n=-\infty}^{+\infty}c_n e^{i \frac{n\pi x}{\lambda}}$
그리고
$a_n=\frac1{\lambda}\int_{-\lambda}^{\lambda} f(x) \cos \frac{n\pi x}{\lambda} dx$
$b_n=\frac1{\lambda}\int_{-\lambda}^{\lambda} f(x) \sin \frac{n\pi x}{\lambda} dx$
$c_n=\frac1{2\lambda}\int_{-\lambda}^{\lambda} f(x) e^{-i \frac{n\pi x}{\lambda}}dx$

공간이 아니라 시간일 때는 $(x\to t,\; \lambda\to T)$ 로만 바꿔주면 됨.


[edit]

4. 기타/관련

다음에서 파동함수가 언급. TOLINK
양자역학,quantum_mechanics
오비탈,orbital - 원자나 분자 내 전자나 전자쌍의 파동함수 인가?? CHK