Difference between r1.15 and the current
@@ -2,7 +2,46 @@
----
R, L, C에서 전압강하는 각각
$V_R=iR$
$V_L=L\frac{di}{dt}$
$V_C=\frac{q}{C}$
인데 전류가
$i=\frac{dq}{dt}$
이므로 다시 쓰면
$V_R=R\frac{dq}{dt}$
$V_L=L\frac{d^2q}{dt^2}$
$V_C=\frac{q}{C}$
이다.
KVL에 따르면 (L R C 순으로 적는 게 좋음)
$V_L+V_R+V_C=\mathcal{E}(t)$
이므로,
$L\frac{d^2q}{dt^2}+R\frac{dq}{dt}+\frac1Cq=\mathcal{E}(t)$
여기서 교류회로라면 $\mathcal{E}(t)=\mathcal{E}_0 \cos \omega t$ 이런 식으로 놓으면 된다.
= 이하 del or cleanup =
[[저항,resistance]]비슷한 그...[[임피던스,impedance]] Z는
$Z=\sqrt{R^2+(X_L-X_C)^2}$
QQQ 병렬rlc와 직렬rlc회로는 어떻게 다른가??
$L\frac{d^2Q}{dt^2}+R\frac{dQ}{dt}+\frac{Q}{C}=0$
= 연대원주 =
회로 방정식은
$\frac{dU}{dt}=-I^2R$
$\frac{dU}{dt}=LI\frac{dI}{dt}+\frac{Q}{C}\frac{dQ}{dt}=-I^2R$
$L\frac{d^2Q}{dt^2}+R\frac{dQ}{dt}+\frac{Q}{C}=0$
풀면
$Q=Q_{\rm max}e^{-\frac{Rt}{2L}}\cos(\omega_d t)$
$\omega_d=\sqrt{\frac1{LC}-\left(\frac{R}{2L}\right)^2}$ : [[각진동수,angular_frequency]]
이것은 절대값이 점점 줄어듦. damping
src [[http://www.kocw.net/home/search/kemView.do?kemId=1299691 hjs]] 인덕턴스(2) 41m
= 이하 old =
= RLC 직렬 회로의.. CHK =
[[리액턴스,reactance]]:
@@ -37,10 +76,6 @@
## from introduction-to-electronic-engineering.pdf @ iPad Acrobat p.12$G=\frac1{X_L}-\frac1{X_C}$
$Z=\sqrt{G^2+\frac1{R^2}}$
RLC 직렬회로(RLC series circuit)에서 각 장치에서의 전압 강하([[전압강하,voltage_drop]])는
L:
@@ -58,6 +93,7 @@
----
[[WpEn:RLC_circuit]]
[[Namu:RLC회로]]
Up: [[아날로그회로,analog_circuit]]
R, L, C에서 전압강하는 각각
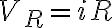
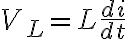
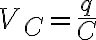
인데 전류가
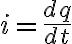
이므로 다시 쓰면
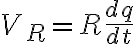
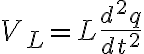
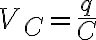
이다.
KVL에 따르면 (L R C 순으로 적는 게 좋음)
)
이므로,
)
여기서 교류회로라면 =\mathcal{E}_0 \cos \omega t) 이런 식으로 놓으면 된다.
이런 식으로 놓으면 된다.
KVL에 따르면 (L R C 순으로 적는 게 좋음)
RLC 직렬 회로의.. CHK ¶
리액턴스,reactance:
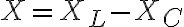
전압,voltage:
^2})
^2})

임피던스,impedance:
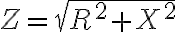
^2})
^2})
(단위 Ω)
여기서
고유 진동수(AKA 공명 진동수) - curr. 진동수,frequency, 고유진동수,natural_frequency LATER
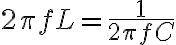 일 때 최대 전류가 흐르며
일 때 최대 전류가 흐르며
 인 교류 전원에 대해서 최대, 이 값이 고유진동수 or 공명진동수
인 교류 전원에 대해서 최대, 이 값이 고유진동수 or 공명진동수
공명진동수,resonance_frequency는
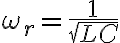
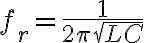
고유 진동수(AKA 공명 진동수) - curr. 진동수,frequency, 고유진동수,natural_frequency LATER


![[http]](/123/imgs/http.png)