RLC 직렬 회로의.. CHK ¶
리액턴스,reactance:
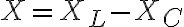
전압,voltage:
^2})
^2})

임피던스,impedance:
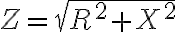
^2})
^2})
(단위 Ω)
여기서
고유 진동수(AKA 공명 진동수) - curr. 진동수,frequency, 고유진동수,natural_frequency LATER
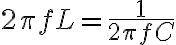 일 때 최대 전류가 흐르며
일 때 최대 전류가 흐르며
 인 교류 전원에 대해서 최대, 이 값이 고유진동수 or 공명진동수
인 교류 전원에 대해서 최대, 이 값이 고유진동수 or 공명진동수
공명진동수,resonance_frequency는
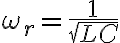
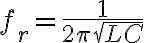
고유 진동수(AKA 공명 진동수) - curr. 진동수,frequency, 고유진동수,natural_frequency LATER


![[http]](/123/imgs/http.png)