Motivation: 우리가 아는 유리수,rational_number는 소숫점 오른쪽으로 무한히 많은 숫자,digit가 있을 수 있다 - 그렇다면 왼쪽으로도 무한히 많은 그런 수와 그 연산, 산술,arithmetic을 생각할 수 있지 않을까?
n-adic number도 있으나 n이 소수,prime_number인 경우가 수학적으로 중요하다. (hence the ‘p’)
MKL
무한급수,infinite_series
modular_arithmetic modular_arithmetic ... rel 법,modulus ... curr 산술,arithmetic?action=highlight&value=modular_arithmetic
modular_arithmetic ... rel 법,modulus ... curr 산술,arithmetic?action=highlight&value=modular_arithmetic
무한급수,infinite_series
modular_arithmetic
// tmp from  수 체계 > p진정수,p진유리수
수 체계 > p진정수,p진유리수
{
p진정수,p-adic_integer
p진 정수 p-adic_integer
p진 유리수 p-adic_rational
{
p진정수,p-adic_integer
p진 정수 p-adic_integer
p-adic integer들의 환,ring : 보통 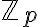 로 표기하며, 이것의 field of fractions 즉
로 표기하며, 이것의 field of fractions 즉 ) 가 바로 p-adic rational들의 체,field로 정의되고
가 바로 p-adic rational들의 체,field로 정의되고 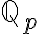 라고 쓴다....
라고 쓴다....
https://everything2.com/title/p-adic integer
https://everything2.com/title/p-adic integers%3A analytic properties
https://proofwiki.org/wiki/Definition:P-adic_Integer
 p진 정수
p진 정수
 p진 정수
p진 정수
 p진 정수
p진 정수
rel 정수,integer
p진유리수,p-adic_rational // _number?https://everything2.com/title/p-adic integer
https://everything2.com/title/p-adic integers%3A analytic properties
https://proofwiki.org/wiki/Definition:P-adic_Integer
rel 정수,integer
p진 유리수 p-adic_rational
p는 임의의 소수,prime_number이고 그에 대해 p-adic rational numbers가 체,field 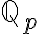 를 이룬다. (nLab)
를 이룬다. (nLab)
https://everything2.com/title/p-adic rational
rel 유리수,rational_number
}https://everything2.com/title/p-adic rational
rel 유리수,rational_number
Topics:
p-adic_norm - 노름,norm에 언급 있음
p-adic_metric
p-adic_order
p-adic_valuation -> see p-adic_order // rel. valuation(writing) 절대값,absolute_value
p-adic_order // rel. valuation(writing) 절대값,absolute_value
p진 절대값 p-adic_absolute_value
p-adic_norm - 노름,norm에 언급 있음
p-adic_metric
https://proofwiki.org/wiki/Definition:P-adic_Metric
 p-adic metric
p-adic metric
metric ... 메이트릭,metric 메트릭,metric 계량,metric 거리,metric 저것의 pagename TBD
p-adic_physicsmetric ... 메이트릭,metric 메트릭,metric 계량,metric 거리,metric 저것의 pagename TBD
p-adic_order
p-adic_valuation -> see
https://everything2.com/title/p-adic valuation
https://proofwiki.org/wiki/Definition:P-adic_Valuation
값매김,valuation
p-adic_analysishttps://proofwiki.org/wiki/Definition:P-adic_Valuation
값매김,valuation
p진 절대값 p-adic_absolute_value
links ko ¶
p진 해석과 기하
1 https://horizon.kias.re.kr/13825/ 수의 크기를 재는 여러 방법?
2 https://horizon.kias.re.kr/14296/ p진수에 대한 소개
4 https://horizon.kias.re.kr/15463/ p진수를 활용한 슬기로운 방정식 풀이 下
5 https://horizon.kias.re.kr/16051/ p진수 함수의 세계
6 https://horizon.kias.re.kr/16184/ p진 기하, 테이트에서 숄체까지
1 https://horizon.kias.re.kr/13825/ 수의 크기를 재는 여러 방법?
2 https://horizon.kias.re.kr/14296/ p진수에 대한 소개
p진 전개를 해서 임의의 유리수,rational_number를 p진수로 표기할 수 있다.
3 https://horizon.kias.re.kr/14918/ p진수를 활용한 슬기로운 방정식 풀이 上4 https://horizon.kias.re.kr/15463/ p진수를 활용한 슬기로운 방정식 풀이 下
5 https://horizon.kias.re.kr/16051/ p진수 함수의 세계
6 https://horizon.kias.re.kr/16184/ p진 기하, 테이트에서 숄체까지
Bmks en ¶
1 Billion is Tiny in an Alternate Universe: Introduction to p-adic Numbers - YouTube
https://www.youtube.com/watch?v=3gyHKCDq1YA
... p-adic.number
p-adic.number
https://www.youtube.com/watch?v=3gyHKCDq1YA
...
Twins:
 p진수
p진수
 p-adic_number
p-adic_number
 p-adic_number
p-adic_number
 p-adic_Number
p-adic_Number
https://mathworld.wolfram.com/p-adicNumber.html
https://mathworld.wolfram.com/p-adicInteger.html
https://ncatlab.org/nlab/show/p-adic number
https://ncatlab.org/nlab/show/p-adic integer
https://encyclopediaofmath.org/wiki/P-adic_number
https://proofwiki.org/wiki/Definition:P-adic_Number
https://mathworld.wolfram.com/p-adicNumber.html
https://mathworld.wolfram.com/p-adicInteger.html
https://ncatlab.org/nlab/show/p-adic number
https://ncatlab.org/nlab/show/p-adic integer
https://encyclopediaofmath.org/wiki/P-adic_number
https://proofwiki.org/wiki/Definition:P-adic_Number

