크기,size
카디널리티,cardinality
측도,measure 측정,measurement
과 관계는? 크기(1D 길이, 2D 넓이, 3D 부피, ...)를 추상화/일반화 한 거 맞음?
카디널리티,cardinality
측도,measure 측정,measurement
과 관계는? 크기(1D 길이, 2D 넓이, 3D 부피, ...)를 추상화/일반화 한 거 맞음?
거리의 일반화가 metric(계량,metric 혹은 거리,metric, writing) (or 거리함수,distance_function)
크기,size의 일반화가 norm (src: 노름(수학)#s-1)
노름(수학)#s-1)
크기,size의 일반화가 norm (src:
절대값의 합은 L1 norm.
일반적인 norm은 L2 norm.
(비교, del ok)
제곱의 합의 제곱근 = norm (L2-norm only)
제곱의 평균의 제곱근 = rms (제곱평균제곱근,root_mean_square,RMS)
일반적인 norm은 L2 norm.
(비교, del ok)
제곱의 합의 제곱근 = norm (L2-norm only)
제곱의 평균의 제곱근 = rms (제곱평균제곱근,root_mean_square,RMS)
L2 norm : square root of the sum of the absolute values squared
^{\frac12})
Lp norm :
^{\frac1p})
L∞ norm : infinity norm? (엄밀한 것은 아니고 기억법?) (|x|∞ + |x|∞ + …)1/∞ 괄호 안에선 가장 큰 것만 살아남는다 - 무한대승이다 보니 가장 큰 것 외에는 모두 무시된다. 그리고 가장 큰 것의 ∞승과 가장 바깥의 1/∞승이 상쇄되어 결국 max()와 같다.[1]
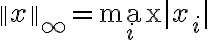
2023-05-24 증명은 이렇다. https://vegatrash.tistory.com/64
2023-05-24 증명은 이렇다. https://vegatrash.tistory.com/64
// tmp from https://aerospacekim.tistory.com/14 마지막부분
정의
2020-11-11
노름(norm)은 길이(length), magnitude와 확실히 깊은 관련.
벡터,vector의 차이,difference의 노름을 거리,distance로 정의하는 듯. 식 추가 TBW.
노름(norm)은 길이(length), magnitude와 확실히 깊은 관련.
벡터,vector의 차이,difference의 노름을 거리,distance로 정의하는 듯. 식 추가 TBW.
이것의 일반화로 valuation { 값매김? 부치? https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=valuation ... rel. 값,value 삼각부등식,triangle_inequality Twins: https://mathworld.wolfram.com/Valuation.html } 이 있음 ... (mw)
Twins:
https://mathworld.wolfram.com/p-adicNorm.html
https://proofwiki.org/wiki/Definition:P-adic_Norm
}
https://mathworld.wolfram.com/p-adicNorm.html
https://proofwiki.org/wiki/Definition:P-adic_Norm
}
2022-02-04
vector_norm
https://planetmath.org/vectornorm
https://planetmath.org/vectorpnorm
p-norm은 (Lp_space Lp-space, aka 르베그_공간,Lebesgue_space, curr at 공간,space) 이거랑 묶어 서술해야하고.. 암튼 현재는 see:
2022-03-16
// ㄷㄱㄱ Week 1-1 p16
p노름,p-norm
{
p-norm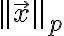
vector_norm
https://planetmath.org/vectornorm
real_vector_space 그리고 complex_vector_space 에서 정의. 방법은 비슷.
p-norm, vector_p-normhttps://planetmath.org/vectorpnorm
p-norm은 (Lp_space Lp-space, aka 르베그_공간,Lebesgue_space, curr at 공간,space) 이거랑 묶어 서술해야하고.. 암튼 현재는 see:
2022-03-16
// ㄷㄱㄱ Week 1-1 p16
p노름,p-norm
{
p-norm
For 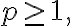 p-norm of
p-norm of 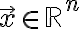 is defined as
is defined as
![$||\vec{x}||_p = \left[ \sum_{i=1}^n \left| x_i \right|^p \right]^{\frac1p}$ $||\vec{x}||_p = \left[ \sum_{i=1}^n \left| x_i \right|^p \right]^{\frac1p}$](/123/cgi-bin/mimetex.cgi?\Large ||\vec{x}||_p = \left[ \sum_{i=1}^n \left| x_i \right|^p \right]^{\frac1p})
특히 자주 나오는 p-노름 세 가지는,
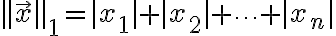
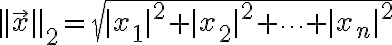
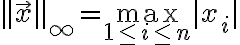
}
Contents
2. L-노름? : L1, L2, ..., Lp, ..., L∞ ¶
사실 많이 본 노름은 2노름 혹은 L2노름. 이런.

L1노름은
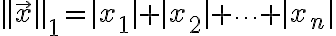
일반화해서
p노름(Lp노름)은
^{\frac1p})
n : 대상이 되는 벡터의 요소 수
p노름(Lp노름)은
인피니티 노름, 상한 노름 : 각 성분의 절대값,absolute_value 중 가장 큰 값을 구하는 노름.
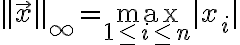
// from https://wikidocs.net/74690 CLEANUP CHK
생각: 이것 비슷한 꼴은
2.1. tmp 1, from ![[http]](/123/imgs/http.png) 가깝다, 멀다 - Distance / Metric의 개념 ¶
가깝다, 멀다 - Distance / Metric의 개념 ¶
(roughly. chk)
L1 norm 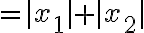
ex. 밥사는데 쓴 돈 + 고기사는데 쓴 돈
ex. 밥사는데 쓴 돈 + 고기사는데 쓴 돈
L2 norm 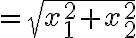
ex. 가로 거리, 세로 거리 (대각선으로 걸어갈 수 있음)
ex. 가로 거리, 세로 거리 (대각선으로 걸어갈 수 있음)
L∞ norm )
ex. 선수A능력치, 선수B능력치 (대표선수 1명만 출전)
ex. 선수A능력치, 선수B능력치 (대표선수 1명만 출전)
Lp norm ![$=\sqrt[p]{|x_1|^p + |x_2|^p}$ $=\sqrt[p]{|x_1|^p + |x_2|^p}$](/123/cgi-bin/mimetex.cgi?\Large =\sqrt[p]{|x_1|^p + |x_2|^p})
2.2. tmp 2; from ![[https]](/123/imgs/https.png) 놈 ¶
놈 ¶
L1 norm - 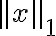 - taxicab norm, Manhattan norm - rel. 맨해튼_거리,Manhattan_distance or taxicab_distance. 벡터의 모든 성분의 절대값의 합
- taxicab norm, Manhattan norm - rel. 맨해튼_거리,Manhattan_distance or taxicab_distance. 벡터의 모든 성분의 절대값의 합
L2 norm -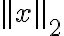 - Euclidean_norm - 벡터의 각 성분을 제곱하고 더해 sqrt
- Euclidean_norm - 벡터의 각 성분을 제곱하고 더해 sqrt
L∞ norm -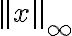 - max_norm - 벡터 성분들의 절대값 중 가장 큰 값
- max_norm - 벡터 성분들의 절대값 중 가장 큰 값
L0 norm -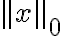 - 벡터 성분 중 0이 아닌 것의 개수
- 벡터 성분 중 0이 아닌 것의 개수
L2 norm -
L∞ norm -
L0 norm -
- 사실 norm이 아님. 조건 세가지를 만족시키지 못함
3. 길이 또는 노름 norm (이하 Kreyszig) ¶
(실내적공간의 공리 세가지와 직교 등은 생략)
실벡터공간 V에 속한 벡터 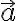 의 길이 또는 노름(norm)은
의 길이 또는 노름(norm)은
}\;\;(\ge 0))
여기서 기본적인 부등식
을 유도할 수 있다고.
을 유도할 수 있다고.
4. Euclid 노름 ¶
5. 함수의 노름 ¶
주어진 구간 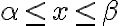 에서 실수값을 갖는 연속함수
에서 실수값을 갖는 연속함수 ,g(x),\cdots) 들의 집합은 일반적인 함수의 덧셈과 스칼라(실수)곱에 의해 실벡터공간을 이룬다. 이 함수공간,function_space 상에서 적분
들의 집합은 일반적인 함수의 덧셈과 스칼라(실수)곱에 의해 실벡터공간을 이룬다. 이 함수공간,function_space 상에서 적분
=\int_{\alpha}^{\beta}f(x)g(x)dx)
를 내적으로 정의할 수 있다. 함수의 노름은
}=\sqrt{\int_{\alpha}^{\beta}f(x)^2 dx})
기 된다.
(이상 세 섹션 Kreyszig 7.9 내적공간,inner_product_space에서. 내적 표기에 a·b 대신 (a,b)를 썼음을 주의. 직접 계산으로 공리 세가지도 확인 가능.)
8. 노름과 내적, 거리함수와의 관계 ¶
tmp {
내적이 정의되면 노름은 그 내적의 제곱근,square_root 값으로 정의되며
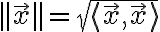
그 역은 성립하지 않는다. 즉,
노름이 있다고 해서 그에 자연스럽게 대응되는 내적이 항상 존재하는 것은 아니다.
내적이 정의되면 노름은 그 내적의 제곱근,square_root 값으로 정의되며
노름이 있다고 해서 그에 자연스럽게 대응되는 내적이 항상 존재하는 것은 아니다.
노름이 정의되면 거리함수,distance_function(혹은 metric) :V\times V\to\mathbb{R}) 가 이렇게 자연스럽게 정의된다.
가 이렇게 자연스럽게 정의된다.
=||\vec{x}-\vec{y}||)
그 역은 성립하지 않는다. 즉,
거리함수가 있다고 해서 그에 자연스럽게 대응되는 노름이 항상 존재하는 것은 아니다. (심지어 거리함수는 벡터공간이 아니라도 정의 가능)
거리함수가 있다고 해서 그에 자연스럽게 대응되는 노름이 항상 존재하는 것은 아니다. (심지어 거리함수는 벡터공간이 아니라도 정의 가능)
내적 → 노름 → 거리함수?
10. 행렬의 노름 ¶
TODO mentioned at 절대값,absolute_value. merge.
TODO 이거 벡터노름(section 1)과 비교. 벡터노름 바로 다음 section으로 옮기는게 나을까?
14. MKLINK: regularization and loss ¶
L1_norm
L2_norm
L2_norm
과 다음 pages를 연결.
L1_regularization
L2_regularization
L2_regularization
L1_loss
L2_loss
L2_loss
정칙화,regularization
{
보이는 다른 번역들:
정규화, (다만 normalization 번역에 쓰이는 단어)
일반화, (다만 generalization 번역에 쓰이는 단어)
{
보이는 다른 번역들:
정규화, (다만 normalization 번역에 쓰이는 단어)
일반화, (다만 generalization 번역에 쓰이는 단어)
15. links ko ¶
https://m.blog.naver.com/ooooooooooo0/220365293655 여기에
노름과 거리,distance 서술,
의 (순서적??) 관계 및
노름의 기호 vs 절대값 기호
내적 표현 괄호 vs 생성집합 표현 괄호
이런 생각들이 있음.
노름과 거리,distance 서술,
의 (순서적??) 관계 및
노름의 기호 vs 절대값 기호
내적 표현 괄호 vs 생성집합 표현 괄호
이런 생각들이 있음.
https://elementary-physics.tistory.com/31 - 교과서적 깔끔 설명
16. links en ¶
http://mathonline.wikidot.com/vector-and-matrix-norms
https://mathworld.wolfram.com/VectorNorm.html
- vector_norm and matrix_norm
vector_normhttps://mathworld.wolfram.com/VectorNorm.html
Frobenius_norm "sometimes also called the Euclidean norm"
https://mathworld.wolfram.com/FrobeniusNorm.html
matrix_norm 의 하나, but "can also be considered as a vector_norm"
matrix의 모든 element들의 제곱을 더한 값? chk
주성분분석,principal_component_analysis,PCA에서 이것의 제곱을 사용? chk
https://mathworld.wolfram.com/FrobeniusNorm.html
matrix_norm 의 하나, but "can also be considered as a vector_norm"
matrix의 모든 element들의 제곱을 더한 값? chk
주성분분석,principal_component_analysis,PCA에서 이것의 제곱을 사용? chk
17. Twins ¶
![[https]](/123/imgs/https.png) 수학백과: 노름
수학백과: 노름https://mathworld.wolfram.com/Norm.html
https://everything2.com/title/norm
https://ncatlab.org/nlab/show/norm
{
1. 에서 정의 두가지로 나누어 설명
On an abelian group // 가환군,commutative_group or 아벨_군,abelian_group ... 저거 페이지명을 뭘로할까? 암튼 curr goto 군,group#s-2.4
On a vector space // 벡터공간,vector_space
}On a vector space // 벡터공간,vector_space
seminorm(writing) 정의 포함.
AKA 놈, 노음, 노옴, 노엄 등. 누가 놂이라고 해도 납득될듯.
Up: 수학,math
----

