무한조화수열,harmonic_sequence을 더한것??
가장 간단한 조화급수
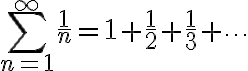
성질: 매우 느리게 발산. 각 항은 0에 가까워지지만 합은 무한대(divergent).
상수 γ ¶
https://mathworld.wolfram.com/Euler-MascheroniConstant.html
https://oeis.org/wiki/Euler–Mascheroni_constant
}
https://oeis.org/wiki/Euler–Mascheroni_constant
}
조화급수를 일반화하면 p급수,p-series (or hyperharmonic series)
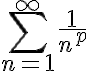
조화급수는 리만_제타함수,Riemann_zeta_function에서 ) 인 경우임.
인 경우임.
조화급수를 일반화하면 리만제타함수.
조화급수를 일반화하면 리만제타함수.
alternating harmonic series ¶
alternating_harmonic_series 는 이런거? chk. (see e2)
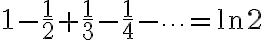
Related:
Bmks ko:
조화 급수(Harmonic Series)와 오일러–마스케로니 상수(Euler–Mascheroni Constant)
https://ghebook.blogspot.com/2010/11/harmonic-series-euler-mascheroni.html
Bmks ko:
조화 급수(Harmonic Series)와 오일러–마스케로니 상수(Euler–Mascheroni Constant)
https://ghebook.blogspot.com/2010/11/harmonic-series-euler-mascheroni.html
Twins:
 조화급수
조화급수
 Harmonic_series_(mathematics)
Harmonic_series_(mathematics)
![[https]](/123/imgs/https.png) https://mathworld.wolfram.com/HarmonicSeries.html
https://mathworld.wolfram.com/HarmonicSeries.html
https://everything2.com/title/harmonic series
![[https]](/123/imgs/https.png) https://mathworld.wolfram.com/HarmonicSeries.html
https://mathworld.wolfram.com/HarmonicSeries.htmlhttps://everything2.com/title/harmonic series

