//from 수학백과: 푸리에 급수
구간,interval![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 정의된 실수값 함수들의 집합,set
에서 정의된 실수값 함수들의 집합,set 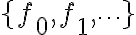 이 다음을 만족하면, 이 집합은 직교집합이다.
이 다음을 만족하면, 이 집합은 직교집합이다.
=\int_a^b f_m(x) f_n(x) dx = 0\;\;\;(m\ne n))
좌변은 내적,inner_product을 뜻한다. 즉 함수의 내적이 0이면 두 함수가 직교한다(직교성,orthogonality)고 정의하는 것.
구간,interval
정의: 직교집합
만약 실수 값을 갖는 함수들의 집합, \phi_1(x), \phi_2(x), \cdots \rbrace) 이 구간
이 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 아래와 같은 관계를 갖는다면 직교한다고 한다.
에서 아래와 같은 관계를 갖는다면 직교한다고 한다.
 = \int_a^b \phi_m(x) \phi_n(x) dx = 0, \; m\ne n)
(Zill 8e ko vol2 p5)
만약 실수 값을 갖는 함수들의 집합
MKLINK
기저,basis
정규직교집합,orthonormal_set - copied to RR at 2023-11-29.
{
orthonormal set
정규직교집합 via orthonormal set
orthonormal set
기저,basis
정규직교집합,orthonormal_set - copied to RR at 2023-11-29.
{
orthonormal set
정규직교집합 via
어떤 벡터  의 놈(norm) 또는 길이
의 놈(norm) 또는 길이 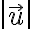 는 내적,inner_product으로 나타낼 수 있다.
는 내적,inner_product으로 나타낼 수 있다.
=\left|\vec{u}\right|^2) 은 제곱놈이라고 한다. 그러므로
은 제곱놈이라고 한다. 그러므로 }) 이다.
이다.
마찬가지로 어떤 함수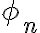 의 제곱놈(square norm)은
의 제곱놈(square norm)은 \right|^2=(\phi_n,\phi_n)) 로 나타낼 수 있다.
로 나타낼 수 있다.
그리고 놈 또는 이 함수의 길이는\right|=\sqrt{(\phi_n,\phi_n)}) 가 된다.
가 된다.
다시 설명하면 직교집합 \right\rbrace) 에 속하는 함수
에 속하는 함수 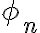 의 제곱놈 또는 놈은 각각 아래와 같다.
의 제곱놈 또는 놈은 각각 아래와 같다.
\right|^2=\int_a^b \phi_n^2(x) dx)
그리고
\right|=\sqrt{\int_a^b \phi_n^2(x) dx})
직교집합  \}) 의 원소
의 원소 ) 가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서
에서 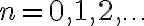 에 대하여
에 대하여  \right|=1) 이면
이면 \}) 를 이 구간 안에서 정규직교 집합(orthonormal set)이라고 한다.
를 이 구간 안에서 정규직교 집합(orthonormal set)이라고 한다.
마찬가지로 어떤 함수
그리고 놈 또는 이 함수의 길이는
다시 설명하면 직교집합
(Zill 8e ko vol2 p5)
}
}
Semi-twins:
![[https]](/123/imgs/https.png) 수학백과: 푸리에 급수 시작부분이 직교집합 정의.
수학백과: 푸리에 급수 시작부분이 직교집합 정의.
![[https]](/123/imgs/https.png) 수학백과: 정규직교기저 앞부분에서 직교집합, 정규직교집합,orthonormal_set, 직교기저,orthogonal_basis, 정규직교기저,orthonormal_basis 설명.
수학백과: 정규직교기저 앞부분에서 직교집합, 정규직교집합,orthonormal_set, 직교기저,orthogonal_basis, 정규직교기저,orthonormal_basis 설명.
![[https]](/123/imgs/https.png) 수학백과: 푸리에 급수 시작부분이 직교집합 정의.
수학백과: 푸리에 급수 시작부분이 직교집합 정의.![[https]](/123/imgs/https.png) 수학백과: 정규직교기저 앞부분에서 직교집합, 정규직교집합,orthonormal_set, 직교기저,orthogonal_basis, 정규직교기저,orthonormal_basis 설명.
수학백과: 정규직교기저 앞부분에서 직교집합, 정규직교집합,orthonormal_set, 직교기저,orthogonal_basis, 정규직교기저,orthonormal_basis 설명.
