(다음 서술 맞는지 CHK!! 완벽하지 않은 부분 있으면 보강할 것)
정사각행렬(n×n행렬) A, 벡터 x, 스칼라값(스칼라,scalar? 상수,constant배?) λ가 있다.
그리고 이런 행렬·벡터 = 스칼라·벡터 관계가 있다.
그리고 이런 행렬·벡터 = 스칼라·벡터 관계가 있다.
A x = λ x
벡터는 영벡터가 아니다. (x ≠ 0) (영벡터라면 너무 당연하게 등식이 성립한다)만약 위 식을 만족시킬 수 없다면, A의 고유벡터와 고유값은 없다.
만약 위 식을 만족시킬 수 있다면, i.e.
식을 만족시키는 벡터 x와 스칼라 λ가 있다면,
그런 벡터 x는 A의 고유벡터,eigenvector이고
그런 스칼라 λ는 A의 고유값,eigenvalue이다.
식을 만족시키는 벡터 x와 스칼라 λ가 있다면,
그런 벡터 x는 A의 고유벡터,eigenvector이고
그런 스칼라 λ는 A의 고유값,eigenvalue이다.
A x = λ x, x ≠ 0 이면 |A - λ I| = 0 이다.
저 (오른쪽의) 방정식을 특성방정식,characteristic_equation이라 하며,
이것은 λ가 미지수인 n차 방정식이며, 풀면 n개의 λ가 나온다. (n개의 근을 보통 이렇게 표기하는 듯. λ1, λ2, … λn) (← 고유값 구하는 방법)
그 λ들을 A x = λ x 에 대입하여 x를 구할 수 있다. (← 고유벡터 구하는 방법)
저 (오른쪽의) 방정식을 특성방정식,characteristic_equation이라 하며,
이것은 λ가 미지수인 n차 방정식이며, 풀면 n개의 λ가 나온다. (n개의 근을 보통 이렇게 표기하는 듯. λ1, λ2, … λn) (← 고유값 구하는 방법)
그 λ들을 A x = λ x 에 대입하여 x를 구할 수 있다. (← 고유벡터 구하는 방법)
기호는 대개 λ, 
여러 개 있는 경우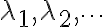 등으로 구분.
등으로 구분.
여러 개 있는 경우
여기서
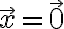 은 한 개의 해가 된다. (이것은 자명. 이 경우를 제외하고,)
은 한 개의 해가 된다. (이것은 자명. 이 경우를 제외하고,)
어떤 벡터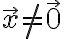 에 대해 식이 성립하는 스칼라
에 대해 식이 성립하는 스칼라  를
를  의 고유값이라 하고,
의 고유값이라 하고,
이 벡터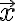 를 고유값
를 고유값  에 대응하는
에 대응하는  의 고유벡터,eigenvector라고 한다.
의 고유벡터,eigenvector라고 한다.
λ는 결정되어야 하는 스칼라,
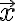 는 결정되어야 하는 벡터이다.
는 결정되어야 하는 벡터이다.
모든 λ에 대해, 어떤 벡터
이 벡터
식을 다시 쓰면
\vec{x}=\vec{0})
이것은  개의 미지수
개의 미지수 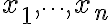 (벡터
(벡터 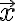 의 성분들)에 대한 선형대수방정식이다. 이 방정식들이
의 성분들)에 대한 선형대수방정식이다. 이 방정식들이 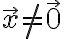 인 해를 갖기 위해서는, 계수행렬
인 해를 갖기 위해서는, 계수행렬 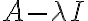 의 행렬식이 0이 되어야 한다. 일단 간단히
의 행렬식이 0이 되어야 한다. 일단 간단히 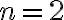 인 경우만 생각하면,
인 경우만 생각하면,
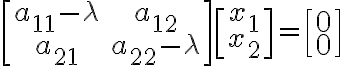
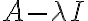 가 특이행렬,singular_matrix이 되기 위한 필요충분조건은 A의 특성행렬식(characteristic determinant)이라 부르는 행렬식,determinant
가 특이행렬,singular_matrix이 되기 위한 필요충분조건은 A의 특성행렬식(characteristic determinant)이라 부르는 행렬식,determinant ) 가 0이 되는 것이다. (일반적인
가 0이 되는 것이다. (일반적인  에 대해서도 마찬가지.) 이것으로부터
에 대해서도 마찬가지.) 이것으로부터
=\begin{vmatrix}a_{11}-\lambda & a_{12} \\ a_{21} & a_{22}-\lambda \end{vmatrix})
(a_{22}-\lambda)-a_{12}a_{21})
\lambda+a_{11}a_{22}-a_{12}a_{21}=0)
λ에 대한 이 이차방정식,quadratic_equation을 행렬 A의 특성방정식,characteristic_equation이라 하며, 이것의 해는 A의 고유값 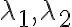 이다. (후략)
이다. (후략)
// mklink 특성다항식,characteristic_polynomial
// mklink 특성다항식,characteristic_polynomial
(Kreyszig 10e 번역판 p159)
수
그 해벡터
tmp def from https://pinkwink.kr/185
물리학에서 고유값 문제란? Eigenvalue Problem
https://freshrimpsushi.tistory.com/1637
{
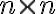 행렬
행렬  가 있을 때, 식
가 있을 때, 식

를 만족하는  행렬
행렬 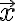 와 상수
와 상수  를 찾는 것을 고유값 문제라고 한다.
를 찾는 것을 고유값 문제라고 한다.
이러한 행렬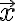 를
를  의 고유함수,eigenfunction라 하고
의 고유함수,eigenfunction라 하고  를
를 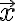 의 고유값이라 한다.
의 고유값이라 한다.
}
https://freshrimpsushi.tistory.com/1637
{
이러한 행렬
}
이름, 명칭 ¶
AKA 특성값(characteristic value), 잠정근(latent root) // characteristic_value latent_root
(고유벡터는 AKA 특성벡터(characteristic vector)) // 고유벡터,eigenvector
n×n 행렬 A의 모든 고유값의 집합을 A의 스펙트럼(spectrum)이라 함. 최대로 서로 다른 n개의 고유값을 가질 수 있음. // 스펙트럼,spectrum
A의 고유값의 절대값의 최대값을 A의 스펙트럼 반경(spectrum radius)이라 함. // 스펙트럼반지름,spectral_radius
// from![[https]](/123/imgs/https.png) https://rfriend.tistory.com/181
https://rfriend.tistory.com/181
(고유벡터는 AKA 특성벡터(characteristic vector)) // 고유벡터,eigenvector
n×n 행렬 A의 모든 고유값의 집합을 A의 스펙트럼(spectrum)이라 함. 최대로 서로 다른 n개의 고유값을 가질 수 있음. // 스펙트럼,spectrum
A의 고유값의 절대값의 최대값을 A의 스펙트럼 반경(spectrum radius)이라 함. // 스펙트럼반지름,spectral_radius
// from
![[https]](/123/imgs/https.png) https://rfriend.tistory.com/181
https://rfriend.tistory.com/181스펙트럼
기호: 행렬 A의 스펙트럼은 λ(A)
행렬,matrix의 스펙트럼,spectrum은, 그 행렬의 고유값,eigenvalue의 집합,set을 뜻함.
https://mathworld.wolfram.com/MatrixSpectrum.html
 Spectrum_of_a_matrix
Spectrum_of_a_matrix
관련 정리: 스펙트럼_정리
스펙트럼_정리  Spectral_theorem .... 스펙트럼정리,spectral_theorem(writing)
Spectral_theorem .... 스펙트럼정리,spectral_theorem(writing)
기호: 행렬 A의 스펙트럼은 λ(A)
행렬,matrix의 스펙트럼,spectrum은, 그 행렬의 고유값,eigenvalue의 집합,set을 뜻함.
https://mathworld.wolfram.com/MatrixSpectrum.html
관련 정리:
고유값과 행렬식,determinant의 관계:
 가
가 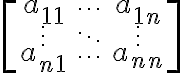 의 고유값이라는 것
의 고유값이라는 것
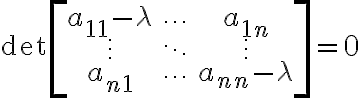
Cramer 정리 관련. 위의
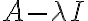 : 특성행렬(characteristic matrix)
: 특성행렬(characteristic matrix)
=\det(A-\lambda I)) : 행렬 A의 특성행렬식(characteristic determinant)
: 행렬 A의 특성행렬식(characteristic determinant)
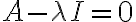 : 특성방정식(characteristic equation) AKA 고유방정식(eigenvalue equation)
: 특성방정식(characteristic equation) AKA 고유방정식(eigenvalue equation)
⇔
n차 정사각행렬의 고유값은 한 개 이상 n개 이하의 서로 다른 값.
순서: 먼저 고유값을 구하고 Gauss소거법으로 그에 대응하는 고유벡터를 구함.
그 다음 고유공간,eigenspace을 정의. (Kreyszig정의)
만일 w와 x가 행렬 A의 같은 고유값,eigenvalue λ에 대한 고유벡터,eigenvector인 경우, w+x (단, x≠-w)와 kx (단, k는 임의의 0 아닌 스칼라)도 고유벡터가 된다. 따라서 같은 고유값 λ에 대응하는 고유벡터들은 0벡터와 함께 하나의 벡터공간,vector_space을 이루며, 이것을 고유값 λ에 대응하는 고유공간(eigenspace)이라고 부른다.
// from https://rfriend.tistory.com/182
고유값 분해 ¶
대각화(Diagonalization)와 고유값분해(eigenvalue decomposition)의 의미 (2019)
https://losskatsu.github.io/linear-algebra/eigen-decomposition/
}
https://losskatsu.github.io/linear-algebra/eigen-decomposition/
}
미분방정식에서 말하는 고유값 ¶
상수 계수 선형 미분방정식,differential_equation의 고유값,eigenvalue은
그 미분방정식의 특성방정식,characteristic_equation(=보조방정식,auxiliary_equation)의 복소근 complex_roots 을 말한다.[1]
그 미분방정식의 특성방정식,characteristic_equation(=보조방정식,auxiliary_equation)의 복소근 complex_roots 을 말한다.[1]
tmp misc facts - chk ¶
- nxn 행렬 고유값은 1, 2, ...., 최대 n개? 중 하나?
- 고유값은 중복이 가능하다
바로 이후에 이어짐 : 이런 경우는 zero-eigenvalues 가 몇 개인가? / 특이값분해,singular_value_decomposition,SVD / ...
tmp links ko ¶
정의: https://rfriend.tistory.com/181 그림 사용하여 eigenvalue + eigenvector 함께 설명.
구하기: https://rfriend.tistory.com/182
구하기: https://rfriend.tistory.com/182
tmp links en ¶
Twins:
![[https]](/123/imgs/https.png) 수학백과: 고윳값
수학백과: 고윳값
https://en.citizendium.org/wiki/Eigenvalue
https://mathworld.wolfram.com/Eigenvalue.html
 eigenvalue
eigenvalue
https://encyclopediaofmath.org/wiki/Eigen_value - of an operator (transformation) of a vector space
of a vector space  over a field
over a field 
![[https]](/123/imgs/https.png) 수학백과: 고윳값
수학백과: 고윳값https://en.citizendium.org/wiki/Eigenvalue
https://mathworld.wolfram.com/Eigenvalue.html
https://encyclopediaofmath.org/wiki/Eigen_value - of an operator (transformation)

