AKA 선형방정식계, 선형연립방정식
해의 개수와... ¶
일반적으로, 연립일차방정식에 대하여 다음 중 하나가 성립한다.
이건 선형시스템의 해집합,solution_set의 카디널리티,cardinality가 세 종류밖에 없다는 것? - CHK
- 유일한 해를 갖는다.
- 해를 갖지 않는다.
- 무수히 많은 해를 갖는다.
이건 선형시스템의 해집합,solution_set의 카디널리티,cardinality가 세 종류밖에 없다는 것? - CHK
연립방정식이 일치(consistent) : 하나 이상의 해가 있음
연립방정식이 불일치(inconsistent) : 해가 없음
연립방정식이 불일치(inconsistent) : 해가 없음
해가 있으면 consistent
해가 없으면 inconsistent
해가 없으면 inconsistent
해,solution의 개수에 따라 세 가지 경우:
위 표의 마지막 열은 다시 말해
해가 존재 : consistent
해가 없음 : inconsistent
consistent (한 해)
consistent (무한히 많은 해) .... TBW 부정방정식,indeterminate_equation과 관계
inconsistent (해 없음)
선형방정식계를 해의 개수에 따라 분류하는 것? - chkconsistent (무한히 많은 해) .... TBW 부정방정식,indeterminate_equation과 관계
inconsistent (해 없음)
| 해가 없음 | 0 | inconsistent |
| 해가 있음, 오직 한 개 | 1 | consistent |
| 해가 있음, 무수히 많이 | ∞ | consistent |
해가 존재 : consistent
해가 없음 : inconsistent

표기법으로 행렬표기법이 있는데 (matrix_notation)
변수들의 계수,coefficient를 가지고 행렬,matrix로 표현하는 것.
그것이
계수행렬,coefficient_matrix
이고, 상수항까지 (오른쪽에?) 포함시키면
첨가행렬,augmented_matrix
CHK
변수들의 계수,coefficient를 가지고 행렬,matrix로 표현하는 것.
그것이
계수행렬,coefficient_matrix
이고, 상수항까지 (오른쪽에?) 포함시키면
첨가행렬,augmented_matrix
CHK
첨가행렬,augmented_matrix을 기본행연산,elementary_row_operation,ERO을 해서
행사다리꼴,row_echelon_form,REF로 변형해서 풀면 가우스_소거,Gaussian_elimination법이라 하고,
기약행사다리꼴,reduced_row_echelon_form,RREF로 변형해서 풀면 Gauss-Jordan 소거법이라 한다.
행사다리꼴,row_echelon_form,REF로 변형해서 풀면 가우스_소거,Gaussian_elimination법이라 하고,
기약행사다리꼴,reduced_row_echelon_form,RREF로 변형해서 풀면 Gauss-Jordan 소거법이라 한다.
....이하 CHK
그리고 변형 과정에서 유일한 해를 갖는지, 해를 가지지 않는지를 알 수 있으며
선행성분의 수 r (계수,rank?) 과 미지수의 수 n의 크기비교도 중요
내용은 다음 사이트 참조.
see https://wikidocs.net/75296
그리고 변형 과정에서 유일한 해를 갖는지, 해를 가지지 않는지를 알 수 있으며
선행성분의 수 r (계수,rank?) 과 미지수의 수 n의 크기비교도 중요
내용은 다음 사이트 참조.
see https://wikidocs.net/75296
관련...
선형방정식,linear_equation (curr goto 방정식,equation)
선형계,linear_system
행렬,matrix
가우스_소거,Gaussian_elimination
TI-Nspire_CAS로 푸는 법: 다음 중 하나를 입력선형계,linear_system
행렬,matrix
가우스_소거,Gaussian_elimination
- rref(첨가행렬,augmented_matrix)
- linSolve(방정식들,{변수들})
2. 표현 ¶
일치와 불일치: 위에서 해의 개수와 관련되므로, 그 바로 뒤에 언급했음.
(또 다른 번역은
(또 다른 번역은
모순이 없다(consistent): 연립방정식이 적어도 하나의 해를 가짐(즉 유일해 또는 무한히 많은 해를 가짐)
모순이 있다(inconsistent): 해를 갖지 않음
이것은 Kreyszig Ch7)모순이 있다(inconsistent): 해를 갖지 않음
제차와 비제차: 중요해서 밑에 section이 있음.
과잉한정(overdetermined): 연립방정식이 미지수보다 더 많은 방정식을 가짐
과소한정(underdetermined): 미지수보다 적은 방정식을 가짐
과소한정(underdetermined): 미지수보다 적은 방정식을 가짐
(Kreyszig Ch7)
4. 행렬의 가역성과 방정식의 해 사이 관계 ¶
(from 고딩 책, easy, del ok)
역행렬,inverse_matrix과 연립일차방정식의 해,solution. 방정식
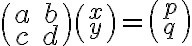
에서,
① 일 때, 오직 한 쌍의 해가 (다음 식) 존재한다.
일 때, 오직 한 쌍의 해가 (다음 식) 존재한다.
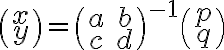
② 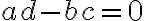 일 때, 해가 무수히 많거나(부정) 해가 없다(불능).
일 때, 해가 무수히 많거나(부정) 해가 없다(불능).
①
5. 풀기 ¶
(행렬)(벡터)=(벡터) 꼴로 먼저 나타낸다.
Ax=b
여기서 A, x, b는 각각 계수행렬coefficient_matrix, 미지수벡터(unknown vector), 상수벡터(constant vector)라 불린다.[1]
Ax=b
여기서 A, x, b는 각각 계수행렬coefficient_matrix, 미지수벡터(unknown vector), 상수벡터(constant vector)라 불린다.[1]
물론 저렇게 하려면 A의 역행렬이 존재해야 한다.
(i.e. A가 가역행렬,invertible_matrix = 정칙행렬,regular_matrix = 비특이행렬 non-singular matrix 이어야 한다.)[2]
(i.e. A가 가역행렬,invertible_matrix = 정칙행렬,regular_matrix = 비특이행렬 non-singular matrix 이어야 한다.)[2]
A의 역행렬이 존재하지 않으면,
(i.e. A가 비가역행렬 non-invertible matrix = 특이행렬,singular_matrix = 퇴화행렬,degenerate_matrix{ 퇴화행렬
퇴화행렬  degenerate_matrix } 이면,)
degenerate_matrix } 이면,)
TBW
(i.e. A가 비가역행렬 non-invertible matrix = 특이행렬,singular_matrix = 퇴화행렬,degenerate_matrix{
TBW
5.1. ERO ¶
선형대수,linear_algebra적 방법...
계수행렬...보다는 첨가행렬,augmented_matrix로 나타낸 다음
기본행연산,elementary_row_operation,ERO 세 연산들을 사용해서
echelon_form 으로 변환하면 답이 보임.
reduced_echelon_form(REF) 으로까지 변환하면 더 명확히 보임.
계수행렬...보다는 첨가행렬,augmented_matrix로 나타낸 다음
기본행연산,elementary_row_operation,ERO 세 연산들을 사용해서
echelon_form 으로 변환하면 답이 보임.
reduced_echelon_form(REF) 으로까지 변환하면 더 명확히 보임.
5.2. Ax=b 풀이법 ... CHK TMP CLEANUP DELME ¶
// https://blog.naver.com/lado135/221879792739 (1)
// https://blog.naver.com/lado135/221884748041 (2)
Ax=b의 해가 존재하기 위한 조건:
1. b가 A의 열공간,column_space안에 있다.
2. 어떤 A의 행의 조합이 영행을 만든다면, 같은 조합으로 b도 0(?)을 만들어야 한다.
둘은 같은 말이라고.
// https://blog.naver.com/lado135/221884748041 (2)
Ax=b의 해가 존재하기 위한 조건:
1. b가 A의 열공간,column_space안에 있다.
2. 어떤 A의 행의 조합이 영행을 만든다면, 같은 조합으로 b도 0(?)을 만들어야 한다.
둘은 같은 말이라고.
미지수가 식보다 많을 경우 모든 해,solution을 찾는 법.
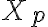 : particular solution
: particular solution
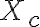 : complete solution
: complete solution
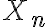 : nullspace solution - see 영공간,null_space
: nullspace solution - see 영공간,null_space
free variables에 0을 넣어서 back substitution을 통해 particular solution) 을 구한다.
을 구한다.
다음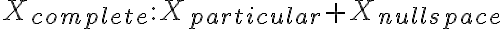
(CLEANUP)
free variables에 0을 넣어서 back substitution을 통해 particular solution
다음
(CLEANUP)
6. 제차연립방정식과 비제차연립방정식 ¶
●
● 하나라도 0이 아니면 비제차연립방정식(nonhomogeneous system).
제차이면, 자명한 해 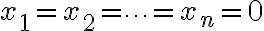 이 있음.
이 있음.
7. 특이해와 제차해 ¶
연립일차방정식,system_of_linear_equations의 해,solution: 특이해와 제차해
예를 들어

↔
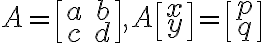
A가 정칙이면, ↔
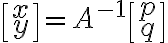
A가 정칙이 아니면
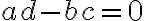
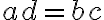
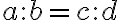
즉 두 직선이 collinear.
예를 들어
두 직선이 일치함(해가 무수히 많음)을 가정하면, 이 연립방정식의 무수히 많은 모든 해를 특이해와 제차해의 조합으로 표현 가능.
특이해: 다음을 만족하는 ^t)
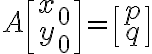
제차해: 위 식에서 우변 상수를 0으로 했을때의 해 ) (단
(단 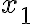 과
과 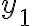 중에 적어도 하나는 0이 아님. 책에선
중에 적어도 하나는 0이 아님. 책에선 \ne(0,0)) 으로 표기.)
으로 표기.)
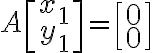
임의의 상수 c에 대해, 다음 ) 는 모두 원래 방정식의 해가 됨
는 모두 원래 방정식의 해가 됨
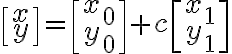
이것은 A를 곱하면 확인 가능
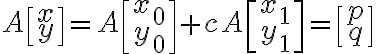
직선으로 나타내면
특이해는 직선상의 한 점에 대응
제차해는 직선 방향을 나타내는 벡터에 대응
(나카이 에츠지)제차해는 직선 방향을 나타내는 벡터에 대응
8. 수반동차연립방정식 ¶
associated homogeneous system of linear equation
Ax=b에 대해 Ax=0을 뜻함. https://wikidocs.net/75598 의 5. 참조.
수반동차연립방정식의 해는 일차연립방정식의 해에 특수해를 더해 얻는다고.
Ax=b에 대해 Ax=0을 뜻함. https://wikidocs.net/75598 의 5. 참조.
수반동차연립방정식의 해는 일차연립방정식의 해에 특수해를 더해 얻는다고.
9. 선형연립방정식과 수반동차연립방정식의 해집합 사이의 관계 ¶
선형연립방정식의 해가 유일함
수반동차연립방정식의 해가 유일해서 영벡터밖에 없음
선형연립방정식의 해가 무수히 많음수반동차연립방정식이 자명하지 않은 해를 가짐
선형연립방정식의 해가 존재하지 않음수반동차연립방정식의 해공간과 별도로 특수한 해 x0가 없다는 것
from https://wikidocs.net/75791; CHK
