Difference between r1.11 and the current
@@ -2,5 +2,10 @@
'''[[극좌표,polar_coordinate]]'''
'''[[극좌표,polar_coordinate]]''' - merge?
[[평면,plane]] 위 [[점,point]]의 [[위치,position]]를,
* [[원점,origin]]으로부터의 [[거리,distance]]와 $(r)$
* 원점 기준 [[방향,direction]](rel. 시초선과의 [[각,angle]]) $(\theta)$
으로 정하는 [[좌표계,coordinate_system]].[* [[https://terms.naver.com/entry.naver?docId=1069419&cid=40942&categoryId=32223 두산백과: 극좌표]]]
'''극좌표계''' (r,θ)와 [[직교좌표계,rectangular_coordinate_system]] (x,y)의 관계 :
$\left.x=r\cos\theta\\y=r\sin\theta\right}\leftrightarrow\left{r^2=x^2+y^2\\ \tan\theta=\frac{y}{x}\right.$
@@ -32,7 +37,37 @@
를 대입하고 정돈하면$x^2+\left(y-\frac{a}{2}\right)^2=\left({a\over 2}\right)^2$
가 된다. 즉 처음 식은 중심이 $(0,a/2)$ 이고 반지름이 $a/2$ 인 [[원,circle]].
같은 페이지에 [[타원,ellipse]]도 있는데 복잡해서 안적음
= 이하 내용 와선 or spiral 으로 분리? =
그럼 pagename TBD.
kms spiral => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral
kms 와선 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=와선 ([[Date(2022-12-24T10:32:08)]]에 none.)
Zeta:와선
WpKo:와선
[[https://terms.naver.com/entry.naver?docId=5669255&cid=60207&categoryId=60207 수학백과: 와선]]
... Google:와선 Google:spiral Naver:와선
= 아르키메데스 와선 =
극좌표계에서 상수 $k$ 에 대하여 식
$r=k\theta$
로 나타내는 곡선을 아르키메데스 와선(spiral)이라 한다. (김홍종)
... Google:아르키메데스+와선
= 쌍곡 와선 =
식
$r=\frac{k}{\theta}$
로 표현. (김홍종)
= 로그 와선 logarithmic spiral =
식
$r=r_0 e^{k\theta}$
로 표현. 여기서 $r_0$ 와 $k$ 는 0이 아닌 상수.
로그 와선은 한바퀴씩 돌 때마다 원점에서의 [[거리,distance]]가 일정한 비율로 나타난다. 또 원점을 지나는 직선과 와선의 각 점에서의 [[접선,tangent_line]]은 항상 일정한 [[각,angle]]을 이루고 있어서, 이 곡선을 등각 와선(equi-angular spiral)이라고도 부른다.
(김홍종)
= gnuplot =
gnuplot에서 극좌표계 모드로 변환하기
@@ -43,10 +78,14 @@
----
Twins:
[[https://terms.naver.com/entry.naver?docId=3536939&cid=60217&categoryId=60217 물리학백과: 극좌표계]]
[[https://terms.naver.com/entry.naver?docId=4125179&cid=60207&categoryId=60207 수학백과: 극좌표계]]
[[WpKo:극좌표계]][[Google:극좌표계]]
[[WpSimple:Polar_coordinate_system]]
[[WpEn:Polar_coordinate_system]][[Google:극좌표계]]
[[Google:Polar+coordinate+system]]Up: [[좌표계,coordinate_system]]
일단은 평면 극좌표계를 다룸
극좌표,polar_coordinate - merge?
평면,plane 위 점,point의 위치,position를,
- 원점,origin으로부터의 거리,distance와
- 원점 기준 방향,direction(rel. 시초선과의 각,angle)
미소 ¶
극좌표계 ) 에서,
에서,
지름 방향의 미소 변화는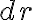 이고, 지름이
이고, 지름이  일 때 중심각 변화
일 때 중심각 변화 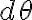 인 호의 길이는
인 호의 길이는  이므로
이므로
미소면적은
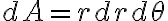
이것을 확장하면 원통좌표계 ) 에선
에선
지름 방향으로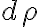 이고, 지름이
이고, 지름이 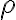 일 때 중심각 변화
일 때 중심각 변화 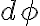 인 호의 길이는
인 호의 길이는 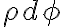 이므로
이므로
xy평면 위의 미소면적은
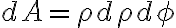
따라서 미소부피는 여기에 높이 방향의 미소 변화량 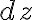 를 곱한
를 곱한
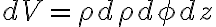
참고로 원통 겉면의 면적소는 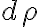 를 빼면 되므로
를 빼면 되므로
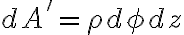
지름 방향의 미소 변화는
미소면적은
지름 방향으로
xy평면 위의 미소면적은
극좌표계에서 원의 표현 ¶
이하 내용 와선 or spiral 으로 분리? ¶
그럼 pagename TBD.
kms spiral => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral
kms 와선 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=와선 (2022-12-24에 none.)
kms spiral => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral
kms 와선 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=와선 (2022-12-24에 none.)
로그 와선 logarithmic spiral ¶
식
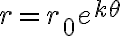
로 표현. 여기서 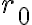 와
와  는 0이 아닌 상수.
는 0이 아닌 상수.
로그 와선은 한바퀴씩 돌 때마다 원점에서의 거리,distance가 일정한 비율로 나타난다. 또 원점을 지나는 직선과 와선의 각 점에서의 접선,tangent_line은 항상 일정한 각,angle을 이루고 있어서, 이 곡선을 등각 와선(equi-angular spiral)이라고도 부른다.
(김홍종)
로그 와선은 한바퀴씩 돌 때마다 원점에서의 거리,distance가 일정한 비율로 나타난다. 또 원점을 지나는 직선과 와선의 각 점에서의 접선,tangent_line은 항상 일정한 각,angle을 이루고 있어서, 이 곡선을 등각 와선(equi-angular spiral)이라고도 부른다.
(김홍종)
gnuplot ¶
gnuplot에서 극좌표계 모드로 변환하기
![[https]](/123/imgs/https.png) https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
set polar
직교 좌표계 모드로 돌아가기set nopolar
(from ![[https]](/123/imgs/https.png) https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
