AKA 다발, 선다발, 플럭스
// MK 다발,flux 플럭스,flux ?
CHK ETYMOLOGY flux#Noun
flux#Noun
CHK TRANSLATION flux
flux  flux
flux  flux
flux
다발=bundle (다발,bundle), 선다발=flux 로 할까? 그냥 플럭스가 최고?
// MK 다발,flux 플럭스,flux ?
CHK ETYMOLOGY
CHK TRANSLATION
다발=bundle (다발,bundle), 선다발=flux 로 할까? 그냥 플럭스가 최고?
기호 Φ, 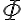
Sub:
자기선속 (자속,magnetic_flux) ΦB
전기선속 (전속,electric_flux) ΦE
선속밀도,flux_density
쇄교자속,flux_linkage λ
질량 플럭스 mass flux = 단위 면적(unit area)를 흐르는 질량 유량 = m / A
Related:전기선속 (전속,electric_flux) ΦE
선속밀도,flux_density
쇄교자속,flux_linkage λ
질량 플럭스 mass flux = 단위 면적(unit area)를 흐르는 질량 유량 = m / A
(related: 연속방정식,continuity_equation)
luminous_fluxluminous flux
광속(luminous flux) ... 빛다발, 광선속 ( luminous flux )
luminous flux )
SI단위: lumen ... 루멘,lumen? lumen#English
lumen#English  Lumen_(unit)
Lumen_(unit)  Lumen_(unit)
Lumen_(unit)  루멘
루멘
 광선속
광선속
 luminous_flux
luminous_flux
 Luminous_flux
Luminous_flux
광속(luminous flux) ... 빛다발, 광선속 (
SI단위: lumen ... 루멘,lumen?
줄여서 lm
1 lm = 1 cd·sr
1 lm = 1 cd·sr
단면적을 통과하는 field의 양
정량적으로 나타낼 때, 보통? or 항상?
- 면적(넓이,area)이 있는 곡면,surface과 (esp. 물론 폐곡면, 닫힌곡면,closed_surface)
- 그것을 뚫고 통과하는 어떤 다발(bundle)
항상 vector field's flux??
physics에서만?
physics에서만?
i.e. flux는 항상 vector field와 연관되는가? 아님 물리에서만 그런가?
2022-07-10
kms flux: "선다발, 유동" via https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=flux
kps flux: 흐름양 유량 선속 선다발 다발 흐름양 via https://www.kps.or.kr/content/voca/search.php?et=en&find_kw=flux (page 7)
kms flux: "선다발, 유동" via https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=flux
kps flux: 흐름양 유량 선속 선다발 다발 흐름양 via https://www.kps.or.kr/content/voca/search.php?et=en&find_kw=flux (page 7)
물리학에서 선속(플럭스)이란?
https://freshrimpsushi.github.io/ko/posts/1991/
단위시간당 단위면적을 지나가는 물리량.
Φ = (물리량,physical_quantity) / (시간,time × 넓이,area).
https://freshrimpsushi.github.io/ko/posts/1991/
단위시간당 단위면적을 지나가는 물리량.
Φ = (물리량,physical_quantity) / (시간,time × 넓이,area).
1.1. 면벡터 ¶
![[http]](/123/imgs/http.png) 면벡터를 먼저 정의해야 함.
면벡터를 먼저 정의해야 함.면벡터: 면을 벡터로 표현한 양
면벡터의 크기: 면의 넓이
면벡터의 방향: 면에 수직인 방향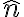
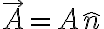
면벡터의 크기: 면의 넓이
면벡터의 방향: 면에 수직인 방향
두 방향 중 한 방향을 마음대로 정한다고 한다 (같은 문제에서는 일관성 있게)
폐곡면의 경우 바깥으로 나가는 방향으로 약속한다고 한다.
면벡터: 폐곡면의 경우 바깥으로 나가는 방향으로 약속한다고 한다.
1.3. 균일하지 않은 벡터장의 선속 ¶
벡터장 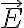 가 균일하지 않으면
가 균일하지 않으면 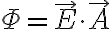 를 이용할 수 없음
를 이용할 수 없음
→ 면벡터를 잘게 나눔
→ 작은 면적소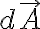 에서는 벡터장이 균일하다고 가정
에서는 벡터장이 균일하다고 가정
→ 작은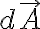 를 지나가는 선속은
를 지나가는 선속은 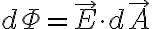
→ 전체 면적 를 통과하는 총 선속은, 모든 면적소를 지나가는 선속을 더해서 얻음
를 통과하는 총 선속은, 모든 면적소를 지나가는 선속을 더해서 얻음
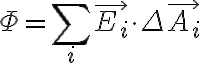
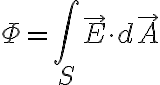
즉 면적분,surface_integral을 함.
→ 면벡터를 잘게 나눔
→ 작은 면적소
→ 작은
→ 전체 면적
폐곡면을 통과하는 균일한 벡터장의 총 선속
(원통이 가로로 놓여있고 벡터장이 왼쪽 원으로 들어가 오른쪽으로 나오는 그림)
오른쪽 단면을 통과하는 선속은
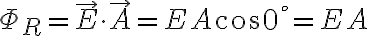
왼쪽 단면을 통과하는 선속은
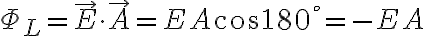
옆면을 통과하는 선속은
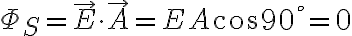
폐곡면을 통과하는(지나가는) 총 선속은
+0=0)
폐곡면 내에서 역선이 생성/소멸되지 않는 한, 어떤 폐곡면이든지 모두 폐곡면을 지나는 총 선속은 항상 0임
(원통이 가로로 놓여있고 벡터장이 왼쪽 원으로 들어가 오른쪽으로 나오는 그림)
오른쪽 단면을 통과하는 선속은
1.4. Fleisch ASGME ¶
The flux of a vector field:
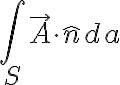
일정한 벡터장(uniform vector field)  및 그에 수직인 곡면,surface S를 가정했을 때, flux
및 그에 수직인 곡면,surface S를 가정했을 때, flux 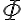 는
는
})
벡터장이 uniform하지만 면에 수직은 아니라면
})
여기서 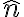 은 단위법선벡터,unit_normal_vector.
은 단위법선벡터,unit_normal_vector.
i번째 조각(segment)의 unit normal은(unit_normal_vector? CHK) 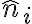 이고 그 면적은
이고 그 면적은 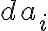 이고, 조각
이고, 조각 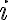 를 통하는(지나는) 흐름은
를 통하는(지나는) 흐름은 da_i) 이고, 전체는
이고, 전체는
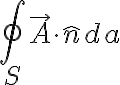
전기장(전기장세기,electric_field_intensity)에 적용하면
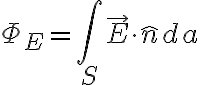
즉 전속,electric_flux
flow through entire surface
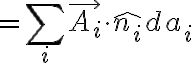
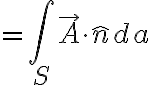
폐곡면이면(A Student's Guide to Maxwell Equations, Fleisch, p10)
2. 전기선속 vs 자기선속 ¶
앙페르_법칙,Ampere_s_law
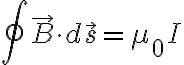
는 B를 선적분,line_integral한것인데,
가우스_법칙,Gauss_s_law처럼 면적분,surface_integral한다면? 결론은 항상 0이다.
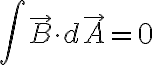
이유는 나간 flux는 항상 다시 들어오기 때문. (자석,magnet의 N/S극을 분리 불가)
그리하여 단일자극은 존재하지 않는다 - 자기 홀극(magnetic monopole)은 존재하지 않는다.
전기선속 전속,electric_flux는 B를 선적분,line_integral한것인데,
가우스_법칙,Gauss_s_law처럼 면적분,surface_integral한다면? 결론은 항상 0이다.
이유는 나간 flux는 항상 다시 들어오기 때문. (자석,magnet의 N/S극을 분리 불가)
그리하여 단일자극은 존재하지 않는다 - 자기 홀극(magnetic monopole)은 존재하지 않는다.
3. etc tmp links ko TOCLEANUP ¶
벡터장의 2D flux (한국어)
https://angeloyeo.github.io/2020/08/18/flux_2D.html
3D flux
https://angeloyeo.github.io/2020/08/21/surface_integral.html
https://angeloyeo.github.io/2020/08/18/flux_2D.html
3D flux
https://angeloyeo.github.io/2020/08/21/surface_integral.html
4. Bazett ¶
이건 (설명을 쉽게 하기 위해서) 3D에서 곡면,surface이 아니라 2D에서 곡선,curve을 지나가는 flux를 설명.
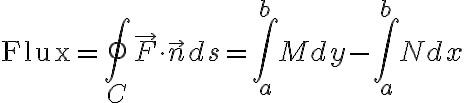
M, N은 그린_정리,Green_theorem를 참조.
6. Misc ¶
어원: flux는 라틴어 유래, 뜻은 흐름(flow). 하지만 단어 flow는 현재 flux와 다른 개념으로 쓰이고 있음에 주의. (See 흐름,flow)
부피흐름률
연속방정식 앞부분에도 flux 설명 있음.
![[https]](/123/imgs/https.png) 물리학백과: 선속 (flux)
물리학백과: 선속 (flux)![[https]](/123/imgs/https.png) 물리학백과: 유체 선속 (fluid flux) m3/s
물리학백과: 유체 선속 (fluid flux) m3/s![[https]](/123/imgs/https.png) 물리학백과: 복사 선속 (radiant flux) J/s 즉 W
물리학백과: 복사 선속 (radiant flux) J/s 즉 Whttps://everything2.com/title/Flux

