베르누이_확률변수,Bernoulli_random_variable

Difference between r1.3 and the current

@@ -2,6 +2,7 @@
$p_0=q=1-p$
$p_1=p$

[[기대값,expected_value]] and [[분산,variance]]:
$\operatorname{E}[X]=p$
$\operatorname{V}[X]=p(1-p)$

@@ -20,10 +21,32 @@
// tmp from [[http://bigdata.dongguk.ac.kr/lectures/med_stat/_book/%ED%99%95%EB%A5%A0%EB%B3%80%EC%88%98%EB%B6%84%ED%8F%AC.html here 2.5.1]]
성공의 확률이 p인 베르누이 실험([[베르누이_시행,Bernoulli_trial]])에서 성공의 횟수를 나타내는 확률변수
즉 확률변수의 영역 $X:\lbrace\mathrm{success,fail}\rbrace\to\lbrace0,1\rbrace$
----
// moved from [[베르누이_시행,Bernoulli_trial]], mklink.
{
성공 확률이 $p$ 인 [[베르누이_시행,Bernoulli_trial]]에서,
[[결과,outcome]]가 성공이면 1, 실패이면 0으로 정의하는 [[확률변수,random_variable]]를
[[모수,parameter]]가 $p$ 인 '''베르누이 확률변수'''(또는 '''베르누이 변수''')라 한다.
$n$ 번째 시행을 나타내는 '''베르누이 확률변수'''를 $X_n$ 이라 하면 다음 내용이 성립.
* $\text{P}(X_n=1)=p$
* $\text{P}(X_n=0)=1-p$
* $\text{E}(X_n)=p$
* $\text{V}(X_n)=p(1-p)$
* 베르누의 변수의 열 $X_1,X_2,\ldots$ 는 상호독립이다. 다시 말해 $n\in\mathbb{N}_1,\,x_i\in\{0,1\}$ 에 대해 다음 식이 항상 성립.
$\text{P}(X_1=x_1,\cdots,X_n=x_n)=\text{P}(X_1=x_1)\cdots\text{P}(X_n=x_n)$
}
----
MKLINK
[[베르누이_과정,Bernoulli_process]]

----
[[https://terms.naver.com/entry.naver?docId=3338164&cid=47324&categoryId=47324 수학백과: 베르누이 확률변수]]

Up: [[이산확률변수,discrete_random_variable]]


$S_X=\{0,1\}$
$p_0=q=1-p$
$p_1=p$


사건,event A에 대한 지시함수,indicator_function IA의 값과 같다.



// tmp from [http]here 2.5.1
성공의 확률이 p인 베르누이 실험(베르누이_시행,Bernoulli_trial)에서 성공의 횟수를 나타내는 확률변수
즉 확률변수의 영역 $X:\lbrace\mathrm{success,fail}\rbrace\to\lbrace0,1\rbrace$

// moved from 베르누이_시행,Bernoulli_trial, mklink.

{
성공 확률이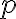 $p$ 인 베르누이_시행,Bernoulli_trial에서,
결과,outcome가 성공이면 1, 실패이면 0으로 정의하는 확률변수,random_variable를
모수,parameter가 $p$ 인 베르누이 확률변수(또는 베르누이 변수)라 한다.

$n$ 번째 시행을 나타내는 베르누이 확률변수를 $X_n$ 이라 하면 다음 내용이 성립.

  • $\text{P}(X_n=1)=p$
  • $\text{P}(X_n=0)=1-p$
  • $\text{E}(X_n)=p$
  • $\text{V}(X_n)=p(1-p)$
  • 베르누의 변수의 열 $X_1,X_2,\ldots$ 는 상호독립이다. 다시 말해 $n\in\mathbb{N}_1,\,x_i\in\{0,1\}$ 에 대해 다음 식이 항상 성립.
    $\text{P}(X_1=x_1,\cdots,X_n=x_n)=\text{P}(X_1=x_1)\cdots\text{P}(X_n=x_n)$

}