단어 '함수'와 '사상'이 비슷하게 쓰이지만, 차이를 든다면 아마도 이거?
{
(공역,codomain이 일반 집합인 함수)를 (공역이 실수체인 실숫값 함수,function)와 구별하여 사상(map, mapping)이라고 부른다. 흔히 정의역과 공역이 일치하는 사상을 변환,transformation이라고 한다.
{
(공역,codomain이 일반 집합인 함수)를 (공역이 실수체인 실숫값 함수,function)와 구별하여 사상(map, mapping)이라고 부른다. 흔히 정의역과 공역이 일치하는 사상을 변환,transformation이라고 한다.
(김홍종 미적1+ p233 6장 2절 선형사상)
}
}
Sub?
Twins:
https://mathworld.wolfram.com/ContinuousMap.html
https://ncatlab.org/nlab/show/continuous map
Up: 연속성,continuity?
}
{ // 여기 내용 local txt로 copied. 여기에 추가하지 말것 //
 로지스틱_사상
로지스틱_사상
 Logistic_map
Logistic_map
https://mathworld.wolfram.com/LogisticMap.html
https://everything2.com/title/logistic map
}
항등사상,identity_map
상수사상,constant_map? - https://mathworld.wolfram.com/ConstantMap.html ( similar: 상수함수,constant_function, curr see 상수,constant 맨아래 ) // del ok
선형사상,linear_map = 선형변환,linear_transformation
연속사상,continuous_map - rel./syn. 연속함수,continuous_function - 둘 다 작성중
{ // 이하 내용 local txt로 copied. 여기에 추가하지 말것 //상수사상,constant_map? - https://mathworld.wolfram.com/ConstantMap.html ( similar: 상수함수,constant_function, curr see 상수,constant 맨아래 ) // del ok
선형사상,linear_map = 선형변환,linear_transformation
연속사상,continuous_map - rel./syn. 연속함수,continuous_function - 둘 다 작성중
Twins:
https://mathworld.wolfram.com/ContinuousMap.html
https://ncatlab.org/nlab/show/continuous map
Up: 연속성,continuity?
}
{ // 여기 내용 local txt로 copied. 여기에 추가하지 말것 //
https://mathworld.wolfram.com/LogisticMap.html
https://everything2.com/title/logistic map
}
bilinear_map - 작성중
quadratic_map - quadratic_map
함자,functor
quadratic_map - quadratic_map
quadratic map
이차사상? 이것은 특정 형태form의 quadratic_recurrence_equation - curr see recurrence_equation - curr see 점화식,recurrence_relation
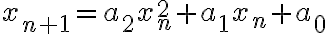
https://mathworld.wolfram.com/QuadraticMap.html
conformal_map or conformal_mapping - 작성중이차사상? 이것은 특정 형태form의 quadratic_recurrence_equation - curr see recurrence_equation - curr see 점화식,recurrence_relation
https://mathworld.wolfram.com/QuadraticMap.html
함자,functor
TBW
전사,surjection AKA 전사함수,surjective_function, onto(위로의 함수)
공역 codomain - 공역,codomain (=공변역)
치역 range - 치역,range
상 image - 상,image
원상 preimage - 원상,preimage (=역상)
전사,surjection AKA 전사함수,surjective_function, onto(위로의 함수)
https://proofwiki.org/wiki/Definition:Surjection
https://en.wikipedia.org/wiki/Surjective_function
https://encyclopediaofmath.org/wiki/Surjection
https://planetmath.org/surjective
공역과 치역이 같음
단사,injection AKA 단사함수,injective_function, one-to-one functionhttps://en.wikipedia.org/wiki/Surjective_function
https://encyclopediaofmath.org/wiki/Surjection
https://planetmath.org/surjective
공역과 치역이 같음
https://proofwiki.org/wiki/Definition:Injection
https://en.wikipedia.org/wiki/Injective_function
https://encyclopediaofmath.org/wiki/Injection
https://planetmath.org/injectivefunction
정의역의 서로 다른 원소를 공역의 서로 다른 원소로 대응
전단사,bijection AKA 전단사함수,bijective_function, one-to-one correspondence(일대일 대응), invertible functionhttps://en.wikipedia.org/wiki/Injective_function
https://encyclopediaofmath.org/wiki/Injection
https://planetmath.org/injectivefunction
정의역의 서로 다른 원소를 공역의 서로 다른 원소로 대응
https://proofwiki.org/wiki/Definition:Bijection
https://en.wikipedia.org/wiki/Bijection
https://encyclopediaofmath.org/wiki/Bijection
https://planetmath.org/bijection
정의역 domain - 정의역,domainhttps://en.wikipedia.org/wiki/Bijection
https://encyclopediaofmath.org/wiki/Bijection
https://planetmath.org/bijection
공역 codomain - 공역,codomain (=공변역)
치역 range - 치역,range
상 image - 상,image
원상 preimage - 원상,preimage (=역상)
함수가 실행하는 사상의 형태에 대한 용어 ¶
| 서로 다른 입력을 서로 다른 출력으로 사상하는 함수 | 일대일 함수 one-to-one function | 단사 함수 injective function |
| 함수가 출력 집합 전체를 덮음 함수의 치역이 함수의 공역과 같음 | 위로의 함수 onto function | 전사 함수 surjective function |
단사라는 용어는 1940년부터 사용했는데, 이는 단사 함수의 작용이 마치 수들이 유체,fluid처럼 흐르는 파이프와 같아 이를 암시한 것이다. 유체는 압축될 수 없으므로,(sic) 출력 공간은 최소한 입력 공간만큼 커야 한다. 단사 함수의 현대적 동의어는 그들이 2대2라고 말하는 것이다. 만약 '입력 유체'에 떠다니는 두 개의 페인트 얼룩을 상상해 보면, 단사 함수는 '출력 유체'에도 두 개의 구별된 페인트 얼룩을 포함할 것이다. 반면 단사가 아닌 함수는 여러 다른 입력을 동일한 출력으로 사상할 수 있다. 예를 들어 =x^2) 은 입력 2, -2가 모두 출력값 4로 사상되기 때문에 단사가 아니다.
은 입력 2, -2가 모두 출력값 4로 사상되기 때문에 단사가 아니다.
See also ¶
http://foldoc.org/map 의 1. - 함수,function와 동의어로 취급.
http://foldoc.org/mapping - redir to http://foldoc.org/function .
http://foldoc.org/mapping - redir to http://foldoc.org/function .
AKA 맵, map, 매핑, mapping 가끔 맵핑
Up: 대수학,algebra

