Difference between r1.14 and the current
@@ -1,5 +1,18 @@
AKA '''Einstein summation convention'''??? 같은건가 sub인가?''[[Date(2022-02-18T02:54:22)]] summation convention 이 더 나은 pagename?''
Chasnov https://youtu.be/CWIaPrwLyjM?si=T8or3V_5-92PhnLY
Ex.
$\sum_{i=1}^3\delta_{ii}\equiv\delta_{ii}=3$
$\epsilon_{ijk}\epsilon_{ijk}=\epsilon_{123}\epsilon_{123}+\cdots=6$
$\epsilon_{ijk}\epsilon_{lmn}=\begin{vmatrix}\delta_{il}&\delta_{im}&\delta_{in}\\\delta_{jl}&\delta_{jm}&\delta_{jn}\\\delta_{kl}&\delta_{km}&\delta_{kn}\end{vmatrix}$
$\vec{A}\cdot\vec{B}=A_iB_i$
$(\vec{A}\times\vec{B})_i = \epsilon_{ijk} A_j B_k$
$\begin{align}(\vec{A}\times\vec{B})_1 &= \epsilon_{1jk} A_j B_k \\ &= \epsilon_{123}A_2B_3 + \epsilon_{132}A_3B_2 \\ &= A_2B_3-A_3B_2\end{align}$
MKL [[크로네커_델타,Kronecker_delta]] [[레비치비타_기호,Levi-Civita_symbol]]
----
MKL
[[합,sum]] (curr goto [[덧셈,addition]])Google:einstein.notation
@@ -80,8 +93,13 @@
https://mathworld.wolfram.com/EinsteinSummation.htmlhttps://freshrimpsushi.github.io/posts/einstein-notation/
https://planetmath.org/einsteinsummationconvention
[[WpEn:Einstein_notation]]
[[WpKo:아인슈타인_표기법]]
chk
https://everything2.com/title/summation+convention
----
Up: [[표기법,notation]]
AKA Einstein summation convention??? 같은건가 sub인가?
2022-02-18 summation convention 이 더 나은 pagename?
2022-02-18 summation convention 이 더 나은 pagename?
Chasnov https://youtu.be/CWIaPrwLyjM?si=T8or3V_5-92PhnLY
Ex.
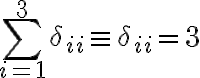

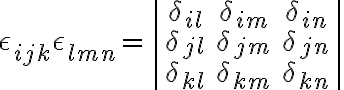
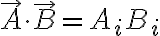
_i = \epsilon_{ijk} A_j B_k)
_1 &= \epsilon_{1jk} A_j B_k \\ &= \epsilon_{123}A_2B_3 + \epsilon_{132}A_3B_2 \\ &= A_2B_3-A_3B_2\end{align})
MKL 크로네커_델타,Kronecker_delta 레비치비타_기호,Levi-Civita_symbol
Ex.
MKL 크로네커_델타,Kronecker_delta 레비치비타_기호,Levi-Civita_symbol
LCY ¶
ex.
일단 전제는

)
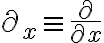
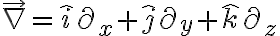
)
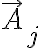 는 A의 j번째 성분????
는 A의 j번째 성분????
이하 파란색이 아인슈타인 표기법으로 표기된 것
일단 전제는
내적,inner_product
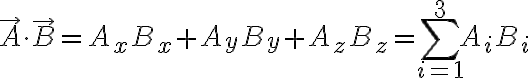
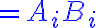
기울기,gradient관련하여
=\hat{i}\partial_x\phi+\hat{j}\partial_y\phi+\hat{k}\partial_z\phi)
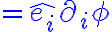
e-hat 표기법은 모르겠는데... 레비치비타_기호,Levi-Civita_symbol의 "벡터곱,vector_product,cross_product에 사용된다는데" 에서 유추해야
발산,divergence관련하여
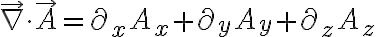
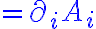
회전,curl
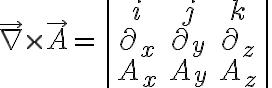
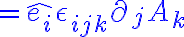
삼중곱,triple_product
=\vec{B}\cdot(\nabla\times\vec{A})-\vec{A}\cdot(\nabla\times\vec{B}))
_i)
)
)
![$=\epsilon_{ijk}\left[(\partial_iA_j)B_k+A_j(\partial_iB_k)\right]$ $=\epsilon_{ijk}\left[(\partial_iA_j)B_k+A_j(\partial_iB_k)\right]$](/123/cgi-bin/mimetex.cgi?\Large =\epsilon_{ijk}\left[(\partial_iA_j)B_k+A_j(\partial_iB_k)\right])
B_k+A_j(\epsilon_{ijk} \partial_i B_k))
_k + A_j (-\epsilon_{jik}\partial_i B_k))
_k + A_j(-(\nabla\times\vec{B})_j))
\cdot\vec{B}-\vec{A}\cdot(\nabla\times\vec{B}))
)
_k)
)
i, j, k는 dummy index이다. 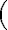 의 왼쪽 ijk와 오른쪽 ijk는 다른 것.
의 왼쪽 ijk와 오른쪽 ijk는 다른 것.
)
)
여기서
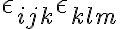
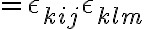
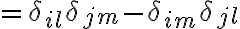
나머지는 H/W라고.
Related:
크로네커_델타,Kronecker_delta
레비치비타_기호,Levi-Civita_symbol
벡터,vector
행렬,matrix matrix_multiplication 대각합,trace
텐서,tensor
내적,inner_product 스칼라곱,scalar_product,dot_product
외적,outer_product 벡터곱,vector_product,cross_product
첨자
https://mathworld.wolfram.com/EinsteinSummation.html
https://freshrimpsushi.github.io/posts/einstein-notation/
https://planetmath.org/einsteinsummationconvention
크로네커_델타,Kronecker_delta
레비치비타_기호,Levi-Civita_symbol
벡터,vector
행렬,matrix matrix_multiplication 대각합,trace
텐서,tensor
내적,inner_product 스칼라곱,scalar_product,dot_product
외적,outer_product 벡터곱,vector_product,cross_product
첨자
위첨자superscript
아래첨자subscript
Twins:아래첨자subscript
https://mathworld.wolfram.com/EinsteinSummation.html
https://freshrimpsushi.github.io/posts/einstein-notation/
https://planetmath.org/einsteinsummationconvention
Up: 표기법,notation


![[http]](/123/imgs/http.png)