안장점,saddle_point

AKA minimax point

어떻게 보면 최소이고 어떻게 보면 최대인 그런..?
최대,maximum 최소,minimum

//from mathworld
정류점,stationary_point이지만 (극값,extremum, 극점,extreme_point)은 아닌 점.
예를 들어 ........를 극값판정법,extremum_test으로.....해보면 안장점이 있다....

//수백
미분가능한 함수에서 임계점,critical_point이지만, 극점,extreme_point(?)이 아닌 점.
see also: 임계점,critical_point#s-4

// ㄷㄱㄱ Week 14-1 p11
{
A 정류점,stationary_point that is neither local maximum nor local minimum is called a saddle point.
국소최대도 국소최소도 아닌 정상점(=정류점)이 안장점.

For a multi-variable function 𝑓(𝒙),
stationary point 𝒙0 with neither positive nor negative semi-definite 𝛻2𝑓(𝒙0) must be a saddle point.
다변수인 경우,
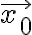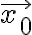$\vec{x_0}$ 에서 $f$ 의 Hessian $\nabla^2 f(\vec{x_0})$ 이 양의준정부호식도 음의준정부호식도 아닌 정상점(=정류점) $\vec{x_0}$ 는 안장점.
// 헤세_행렬,Hessian_matrix

Note: Stationary point 𝒙0 with 𝑓′′(𝑥0) = 0 or 𝛻2𝑓(𝒙0) = 𝟎 may or may not be a saddle point.
QQQ second_derivative 로는 알 수 없다는 얘기? chk
}

Example

plot 3d y^2-x^2 - Wolfram|Alpha
https://www.wolframalpha.com/input?i=plot 3d y^2-x^2
$f(x,y)=y^2-x^2$ 에서 일계미분이 0인 점을 구하면
$f_x=-2x=0,$
$f_y=2y=0$ 에서 $(0,0)$



Sub:
미니맥스원리,minimax_principle
{
minimax principle

Sub:
Courant_minimax_principle { WtEn:Courant_minimax_principle "Courant minimax principle" Ggl:Courant minimax principle } // Courant minimax principle



"minimax principle"
Ndict:minimax principle
Ggl:minimax principle
Up: 원리,principle
} // 미니맥스원리 minimax principle


Ndict:minimax
Ggl:minimax
} // minimax

Sub:
game_saddle_point
{
game saddle point
https://mathworld.wolfram.com/GameSaddlePoint.html
"game saddle point"
Ggl:game saddle point
} // game saddle point




----