pagename 고민. TBD
정수론,number_theory의 cofactor를 여인수, - is a 인수,factor
선대의 cofactor를 여인자 - 여인자,cofactor - is a 인자,factor
이렇게 할까??
후자도 수,number이긴 하다.
정수론,number_theory의 cofactor를 여인수, - is a 인수,factor
선대의 cofactor를 여인자 - 여인자,cofactor - is a 인자,factor
이렇게 할까??
후자도 수,number이긴 하다.
{
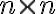 차 행렬식,determinant에서 성분
차 행렬식,determinant에서 성분 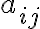 가 속한 행과 열을 없앤 행렬식
가 속한 행과 열을 없앤 행렬식 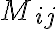 를
를 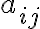 의 소행렬식,minor_determinant이라고 한다. 그리고
의 소행렬식,minor_determinant이라고 한다. 그리고 ^{i+j}M_{ij}) 를
를 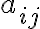 의 여인수(is-a 여인자)라고 한다.
의 여인수(is-a 여인자)라고 한다.
//mw Cofactor 대충번역 at 2022-01-29
(분야: 행렬/linalg)
다른 type의 cofactor - 가끔 cofactor_matrix 라고도 불리는 - 것은 minor { https://mathworld.wolfram.com/Minor.html }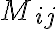 에 부호가 붙은(signed) 버전이며 다음과 같이 정의된다.
에 부호가 붙은(signed) 버전이며 다음과 같이 정의된다.
^{i+j} M_{ij})
이것은 다음과 같이 행렬,matrix  의 행렬식,determinant을 계산하는 데 쓰인다.
의 행렬식,determinant을 계산하는 데 쓰인다.
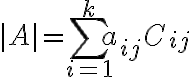
다른 type의 cofactor - 가끔 cofactor_matrix 라고도 불리는 - 것은 minor { https://mathworld.wolfram.com/Minor.html }
1. 사전지식: 소행렬, 소행렬식 ¶
먼저 소행렬과 소행렬식에 대해 행렬,matrix페이지 보다는 여기에 적음.
CHK
{
소행렬(minor matrix)
![[https]](/123/imgs/https.png) 수학백과: 소행렬식
수학백과: 소행렬식
{
소행렬(minor matrix)
n차 정사각행렬에서 i행과 j열을 제거해서 얻어지는 n-1차 정사각행렬
Mij로 표기.
소행렬식(minor determinant)Mij로 표기.
det(Mij) or |Mij| or Dij
소행렬의 행렬식,determinant. 여인수,cofactor계산 시 나오는...![[https]](/123/imgs/https.png) 수학백과: 소행렬식
수학백과: 소행렬식위와 같이 구분하지 않고, 소행렬식을 그냥 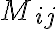 로 표시하기도 함.
로 표시하기도 함.
// http://blog.naver.com/mykepzzang/221080004072 :
n×n행렬 A의 i행과 j열을 제외시킨 부분행렬의 행렬식을 Mij라 쓰고,
Mij를 행렬 A의 성분 aij의 소행렬식이라 한다.
그리고 수^{i+j}M_{ij}) 를 성분
를 성분 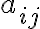 의 여인수라 한다.
의 여인수라 한다.
n×n행렬 A의 i행과 j열을 제외시킨 부분행렬의 행렬식을 Mij라 쓰고,
Mij를 행렬 A의 성분 aij의 소행렬식이라 한다.
그리고 수
정리: ((원소)×(여인수) 곱의 일정성??)
n×n 행렬 A의 어떤 행 또는 열을 선택하는가와 상관없이, 선택된 행 또는 열에 있는 각 원소와 대응하는 여인수의 곱을 모두 더하여 얻은 수는 항상 같다.
n×n 행렬 A의 어떤 행 또는 열을 선택하는가와 상관없이, 선택된 행 또는 열에 있는 각 원소와 대응하는 여인수의 곱을 모두 더하여 얻은 수는 항상 같다.
정의:
행렬 A가 n×n 행렬일 때, A의 임의의 한 행 또는 열에 있는 각 원소와 대응하는 여인수의 곱을 모두 더해 얻은 수를 행렬 A의 행렬식,determinant이라 한다.
이 때 합 자체는 A의 여인수 전개라고 불린다.
행렬 A가 n×n 행렬일 때, A의 임의의 한 행 또는 열에 있는 각 원소와 대응하는 여인수의 곱을 모두 더해 얻은 수를 행렬 A의 행렬식,determinant이라 한다.
이 때 합 자체는 A의 여인수 전개라고 불린다.
i행에 의한 여인수 전개
=a_{i1}C_{i1}+a_{i2}C_{i2}+\cdots+a_{in}C_{in})
(행은 i로 일정하고 모든 열에 대해 더함)
j열에 의한 여인수 전개
=a_{1j}C_{1j}+a_{2j}C_{2j}+\cdots+a_{nj}C_{nj})
(열은 j로 일정하고 모든 행에 대해 더함)
그리고 위 둘, 행에 의한 여인수전개 값과 열에 의한 여인수전개 값은 일치한다.
}
(행은 i로 일정하고 모든 열에 대해 더함)
(열은 j로 일정하고 모든 행에 대해 더함)
}
2. 여인수, 여인자 ¶
Cij = (-1)i+j·det(Mij)
^{i+j}|M_{ij}|)
즉 Cij는 하나의 실수이다.
즉 Cij는 하나의 실수이다.
부호는 당연히, 다음 패턴이다. 예를 들어 5x5행렬이라면,
+−+−+
−+−+−
+−+−+
−+−+−
+−+−+ (checkerboard)
+−+−+
−+−+−
+−+−+
−+−+−
+−+−+ (checkerboard)
여인수행렬, cofactor matrix:
모든 i, j에 대해 Cij들을 모아 행렬을 만든 것?
모든 i, j에 대해 Cij들을 모아 행렬을 만든 것?
여인수전개, cofactor expansion AKA 라플라스 전개, Laplace expansion:
행렬식을 여인수의 결합으로 표현하는 형태
{
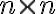 크기 행렬
크기 행렬 ![$A=[a_{ij}]$ $A=[a_{ij}]$](/123/cgi-bin/mimetex.cgi?\Large A=[a_{ij}]) 에 대해, 행렬식은
에 대해, 행렬식은
=a_{11}C_{11}+a_{12}C_{12}+\cdots+a_{1n}C_{1n})
임의의 행을 따라서도 가능하다. 제 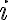 행을 따라 여인수 전개한 행렬식은
행을 따라 여인수 전개한 행렬식은
열을 기준으로도. 제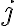 열을 따라...
열을 따라...
내용은 밑의 수학백과 참조.
행렬식을 여인수의 결합으로 표현하는 형태
{
열을 기준으로도. 제
내용은 밑의 수학백과 참조.
그리고 그와 별도로 twins
 라플라스_전개 라플라스 전개(Laplace expansion) 또는 여인자 전개(cofactor expansion)
라플라스_전개 라플라스 전개(Laplace expansion) 또는 여인자 전개(cofactor expansion)
 Laplace_expansion also called cofactor expansion
Laplace_expansion also called cofactor expansion
 라플라스 전개
라플라스 전개
3. 활용: 역행렬 구하기 ¶
그리하여 이것으로 역행렬을 구하기... tmp from ![[http]](/123/imgs/http.png) src p34
src p34
n×n행렬![$A=[a_{jk}]$ $A=[a_{jk}]$](/123/cgi-bin/mimetex.cgi?\Large A=[a_{jk}]) 의 역행렬은
의 역행렬은
![$A^{-1}=\frac1{\det A}[C_{jk}]=\frac1{\det A}\begin{bmatrix}C_{11}&\cdots&C_{n1}\\ \vdots &\ddots &\vdots \\ C_{1n} &\cdots & C_{nn}\end{bmatrix}$ $A^{-1}=\frac1{\det A}[C_{jk}]=\frac1{\det A}\begin{bmatrix}C_{11}&\cdots&C_{n1}\\ \vdots &\ddots &\vdots \\ C_{1n} &\cdots & C_{nn}\end{bmatrix}$](/123/cgi-bin/mimetex.cgi?\Large A^{-1}=\frac1{\det A}[C_{jk}]=\frac1{\det A}\begin{bmatrix}C_{11}&\cdots&C_{n1}\\ \vdots &\ddots &\vdots \\ C_{1n} &\cdots & C_{nn}\end{bmatrix})
![[https]](/123/imgs/https.png) src
src
정사각행렬 A의,
역행렬:
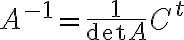 (Cijt 맞나? 그렇게 표현하는 게 낫지 않나? CHK)
(Cijt 맞나? 그렇게 표현하는 게 낫지 않나? CHK)
where^{i+j}M_{ij})
행렬식:
^{i+j}A_{ij}\cdot\det(M_{ij}))
https://www.youtube.com/watch?v=bHdzkFrgRcA 끝부분에 있음 나중에 받아적을것 and cp to MIT_Multivariable_Calculus lec 3 Denis Auroux
1. minors (소행렬을 구한다)
2. cofactors (여인수행렬을 구한다)
3. transpose (전치행렬을 구한다)
4. divide by determinant
![[http]](/123/imgs/http.png) src p34
src p34n×n행렬
![[https]](/123/imgs/https.png) src
src정사각행렬 A의,
역행렬:
where
1. minors (소행렬을 구한다)
2. cofactors (여인수행렬을 구한다)
3. transpose (전치행렬을 구한다)
4. divide by determinant

