이항계수,binomial_coefficient

Difference between r1.17 and the current

@@ -2,9 +2,25 @@
----
rel, mklink
[[이항정리,binomial_theorem]]
[[이항전개,binomial_expansion]]에서 나옴
[[조합,combination]]

[[파스칼의_삼각형,Pascal_s_triangle]]
[[파스칼_삼각형,Pascal_triangle]]
----
(상식으로 대충 적음, CHK and rewrite)
이것은 [[전개,expansion]](esp [[이항전개,binomial_expansion]])공식에서 나오는 [[계수,coefficient]]를 일반적인 n차에 대해 식으로 나타낸 것?
일단 n차를 알아보기 전에 간단한 경우인 n=1,2,3,...부터 보면, 그리고 앞에 0차도 추가하면
||(a+b)^^0^^=1 || 1 ||
||(a+b)^^1^^=a+b || 1 1 ||
||(a+b)^^2^^=a^^2^^+2ab+b^^2^^|| 1 2 1 ||
||(a+b)^^3^^=a^^3^^+3a^^2^^b+3ab^^2^^+b^^3^^ || 1 3 3 1 ||
이렇게 [[파스칼_삼각형,Pascal_triangle]]이 나오며
일반적인 경우는 [[조합,combination]]으로 계산한다.
(a+b)^^n^^에서 a^^n−k^^b^^k^^의 계수는 ,,n,,C,,k,,이다.
그리고 '''이항계수'''를 사용한 [[전개,expansion]]에서 나오는 계수를 설명하는 [[이항정리,binomial_theorem]]는
(a+b)^^n^^ = ,,n,,C,,0,, a^^n^^ + ,,n,,C,,1,, a^^n−1^^ b + ,,n,,C,,2,, a^^n−2^^ b^^2^^ + … + ,,n,,C,,k,, a^^n−k^^ b^^k^^ + … + ,,n,,C,,n,, b^^n^^
## via: 통계가 빨라지는 수학력 - 이항계수 ; chk

----
n개 중에서 k개를 선택하는 [[조합,combination]]의 수
@@ -25,8 +41,14 @@
[[계승,factorial]]의 성질에서 $0!=1$ 이므로
$\binom{n}{0}=\binom{n}{n}=1$

[[이항전개,binomial_expansion]]에서 나옴
= tmp bmks ko =
이항계수의 빠른 계산
https://www.secmem.org/blog/2019/12/14/fast-binomial-calculation/
// [[Chinese_remainder_theorem]], [[스털링_수,Stirling_number]] 언급

----
tmp twins (del)
https://everything2.com/title/binomial+coefficient

Twins
[[https://terms.naver.com/entry.naver?docId=3338178&ref=y&cid=47324&categoryId=47324 수학백과: 이항계수]]
@@ -38,5 +60,4 @@
https://encyclopediaofmath.org/wiki/Binomial_coefficients

Up: Google:binomiality ? Google:binomial ? 암튼 [[WpEn:Binomial]], [[계수,coefficient]]


기호: 다양한데 tbw


(상식으로 대충 적음, CHK and rewrite)
이것은 전개,expansion(esp 이항전개,binomial_expansion)공식에서 나오는 계수,coefficient를 일반적인 n차에 대해 식으로 나타낸 것?
일단 n차를 알아보기 전에 간단한 경우인 n=1,2,3,...부터 보면, 그리고 앞에 0차도 추가하면
(a+b)0=1 1
(a+b)1=a+b 1 1
(a+b)2=a2+2ab+b2 1 2 1
(a+b)3=a3+3a2b+3ab2+b3 1 3 3 1
이렇게 파스칼_삼각형,Pascal_triangle이 나오며
일반적인 경우는 조합,combination으로 계산한다.
(a+b)n에서 an−kbk의 계수는 nCk이다.
그리고 이항계수를 사용한 전개,expansion에서 나오는 계수를 설명하는 이항정리,binomial_theorem는
(a+b)n = nC0 an + nC1 an−1 b + nC2 an−2 b2 + … + nCk an−k bk + … + nCn bn

n개 중에서 k개를 선택하는 조합,combination의 수
이것을 binomial coeffient라고 하며
$\binom{n}{k}:=\frac{n!}{k!(n-k)!}=C^n_k$
영어로는 "n choose k"라고 읽는다.

더 경우가 많아지면(?) 더 일반화하면
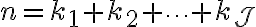$n=k_1+k_2+\cdots+k_{\mathcal{J}}$ 일 때
$\frac{n!}{k_1!k_2!\cdots k_{\mathcal{J}}!}$
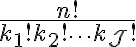
이것을 다항계수,multinomial_coefficient라고 함.
binomial coefficient는 multinomial coefficient에서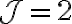 $\mathcal{J}=2$ 인 경우임.
see also: multinomial probability law - curr. goto 확률,probability

(Leon-Garcia)

계승,factorial의 성질에서 $0!=1$ 이므로
$\binom{n}{0}=\binom{n}{n}=1$

[edit]

tmp bmks ko