비공식적 정의:
공간,space에서 점,point을 지정/명시(specify)하기 위한 최소 좌표,coordinate 개수
점의 위치,position를 정의하는 독립적인 매개변수(parameter)나 좌표 수
('좌표 수'가 아니라 '좌표를 구성하는 수의 개수'가 아닌지? chk)점의 위치,position를 정의하는 독립적인 매개변수(parameter)나 좌표 수
1차원 수직선 number_line
2차원
3차원
n차원
위의 이것들은 각각 실수,real_number집합의 곱집합,product_set으로 볼 수 있는?
2차원 평면에 대응하는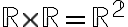
3차원 공간에 대응하는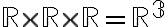 [1]
[1]
2차원
3차원
공간,space - 3차원 space만을 space라 하기도 하고, (공간의 좁은 의미) 혹은 3차원 이상을 space라 하기도 하고, 1·2차원을 포함한 임의의 n차원을 일반화해 모두 space라 하기도 하는 듯. (공간의 넓은 의미) 그리고 Euclidean이 아닌 경우까지도 일반화해 공간이라는 단어를 쓰는 듯. (더 넓은 일반화된 의미?) CHK
4차원초공간,hyperspace? - 4차원 이상을 보통 이렇게 표현하는 듯. CHK -> 이건 n≥4의 명칭이기도 하나 임의의 n차원으로의 일반화,generalization이기도 함, 여러 뜻으로 쓰이는 단어.  Hyperspace_(disambiguation)
Hyperspace_(disambiguation)  hyperspace
hyperspace
...n차원
위의 이것들은 각각 실수,real_number집합의 곱집합,product_set으로 볼 수 있는?
2차원 평면에 대응하는
3차원 공간에 대응하는
보통  차원 Euclidean space? or
차원 Euclidean space? or  - D 좌표계,coordinate_system? 를
- D 좌표계,coordinate_system? 를  으로 표기 - chk
으로 표기 - chk
n차원 유클리드_공간,Euclidean_space을 ℝn으로 표기. chk
n차원 유클리드_공간,Euclidean_space을 ℝn으로 표기. chk
| 차원 | ? | n-dimensional object의 예 | in CG and spatial data | 속성? measure? |
| 0D | point? | point? | point | ? |
| 1D | line?, curve | line | line or polyline | 길이,length |
| 2D | plane | square | polygon | 넓이,area |
| 3D | solid?? | cube | surface | 부피,volume |
| 4D | ? | tesseract | ? | |
| nD | Euclidean n-space? | ? |
QQQ 위의 것은 좌표의 각 값이 연속적인 차원 얘기고 // 실수,real_number 연속성,continuity
1D 스칼라,scalar
2D 벡터,vector
3D 행렬,matrix
nD 텐서,tensor
이것들은 좌표의 각 값이 이산적인 차원?? // 이산성,discreteness
각 원소,element의 인덱스,index는 whole number이므로?
이 생각이 맞는건지?
Contents
- 1. 대수학, 선형대수학의 차원
- 2. 물리의 차원분석(dimensional analysis)
- 3. 차원이 같지만 다른 것(물리개념)들
- 4. Dimensionless
- 5. 영차원 zero_dimension
- 6. 일차원 one_dimension
- 7. 이차원 etc ... n차원
- 8. multidimensional
- 9. 무한차원 (삭제무방)
- 10. 위상적 차원 topological dimension, 르베그 차원 Lebesgue dimension, 르베그 덮개 차원 Lebesgue covering dimension
- 11. 크룰 차원 Krull dimension
- 12. 귀납차원? 귀납적차원? inductive dimension
- 13. dimension invariant
- 14. Minkowski dimension
- 15. Hausdorff dimension
- 16. dimensionality
- 17. dimension reduction / dimensionality reduction
- 18. nondimensionalization
- 19. Sites
- 20. Bmks ko
- 21. Bmks en
1. 대수학, 선형대수학의 차원 ¶
벡터공간 V에 속한 선형독립,linear_independence인 벡터들의 최대 수를 V의 차원이라 부르고 dim V로 표기한다. (Kreyszig)
정의:
{
벡터공간,vector_space V가 n개의 vector로 이루어진 basis를 갖는다면, V는 n차원이다.
} https://beckho.tistory.com/17
집합,set S가 벡터공간,vector_space V의 한 기저,basis일 때,
S에 속하는 벡터,vector의 개수를 V 의 차원(dimension)이라 하며 dimV로 나타낸다.
정리:S에 속하는 벡터,vector의 개수를 V 의 차원(dimension)이라 하며 dimV로 나타낸다.
집합 V가 n-차원 벡터공간일 때, n개의 벡터들의 집합
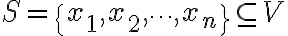
에 대하여 다음이 성립한다.
CHK (1) 집합 S가 일차독립이면 S는 V의 기저이다. (See (일차독립에 대해선 curr. see 선형성,linearity), 선형독립,linear_independence, 기저,basis)
(2)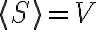 이면 S는 V의 기저이다. (See 생성,span, 생성집합,spanning_set)
이면 S는 V의 기저이다. (See 생성,span, 생성집합,spanning_set)
(2)
{
벡터공간,vector_space V가 n개의 vector로 이루어진 basis를 갖는다면, V는 n차원이다.
} https://beckho.tistory.com/17
벡터공간의 차원
벡터공간,vector_space이란  처럼 원소의 합과 상수배가 정의되어 있는 집합을 말한다. 이때 이 집합의 원소를 벡터,vector라고 부른다. 좌표공간에서처럼 일반적인 벡터공간 V에서도 기저,basis를 말할 수 있다. 이때 벡터
처럼 원소의 합과 상수배가 정의되어 있는 집합을 말한다. 이때 이 집합의 원소를 벡터,vector라고 부른다. 좌표공간에서처럼 일반적인 벡터공간 V에서도 기저,basis를 말할 수 있다. 이때 벡터
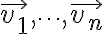
이 V의 기저이고, 또 벡터
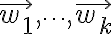
도 V의 기저이면,
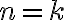
이다. 이 공통값을 V의 차원이라고 부른다.
특히 의 차원은
의 차원은  이다.
이다.
벡터공간의 차원은 일차독립(=선형독립,linear_independence)인 벡터들의 최대 개수와 같다.
특히
벡터공간의 차원은 일차독립(=선형독립,linear_independence)인 벡터들의 최대 개수와 같다.
(김홍종 미적1+ p217 5장 벡터, 6.5 벡터공간의 차원)
2. 물리의 차원분석(dimensional analysis) ¶
L 길이,length (거리,distance, 깊이 depth, 높이 height, 폭 너비 width breadth 등)
M 질량,mass
T 시간,time
Θ 온도,temperature
M 질량,mass
T 시간,time
Θ 온도,temperature
길이 length ![$[x]$ $[x]$](/123/cgi-bin/mimetex.cgi?\Large [x]) [x] = L
[x] = L
넓이 area![$[A]$ $[A]$](/123/cgi-bin/mimetex.cgi?\Large [A]) [A] = L2
[A] = L2
부피 volume![$[V]$ $[V]$](/123/cgi-bin/mimetex.cgi?\Large [V]) [V] = L3
[V] = L3
시간 time![$[t]$ $[t]$](/123/cgi-bin/mimetex.cgi?\Large [t]) [t] = T
[t] = T
속도 velocity![$[v]$ $[v]$](/123/cgi-bin/mimetex.cgi?\Large [v]) [v] = L/T = L T-1
[v] = L/T = L T-1
가속도 acceleration![$[a]$ $[a]$](/123/cgi-bin/mimetex.cgi?\Large [a]) [a] = L/T2 = L T-2
[a] = L/T2 = L T-2
넓이 area
부피 volume
시간 time
속도 velocity
가속도 acceleration
관련: 단위,unit
3.1. 차원이 같은데 스칼라와 벡터로 나뉘는 것들 ¶
같은 차원인데 스칼라와 벡터로 나뉘는 것들.
(단위는 같기도 하고 다르기도 함.)
벡터쪽에는 벡터기호가 붙기도 하고 안붙기도 함. 밑에는 생략. 스칼라쪽엔 당연히 안 붙음.
// 자주 언급되는 것만. 차원이 같은 것들은 너무 많음.
// QQQ 첫줄은 열,heat 에너지,energy 도 차원은 같은데 / 둘째줄은 진동수,frequency .... 등등. 어떤 관련인지... 너무 쓸데없나? DELME
// TMP; CHK; Compiled at 2020-10-25
// 별로 중요하거나 엄밀한 내용은 아닌 듯, 나중에 삭제가능. 이걸 정리하려면 유사벡터=준벡터=pseudovector 등등 더 익혀야 하는게 많음.
(단위는 같기도 하고 다르기도 함.)
벡터쪽에는 벡터기호가 붙기도 하고 안붙기도 함. 밑에는 생략. 스칼라쪽엔 당연히 안 붙음.
| dimension | scalar | vector |
| M L2 T−2 | 일,work W (J) | 토크,torque τ (N·m) |
| T−1 | 각진동수,angular_frequency ω (rad/s) | 각속도,angular_velocity ω (rad/s) |
| L T−1 | 속력,speed v (m/s2) | 속도,velocity v (m/s2) |
// 자주 언급되는 것만. 차원이 같은 것들은 너무 많음.
// QQQ 첫줄은 열,heat 에너지,energy 도 차원은 같은데 / 둘째줄은 진동수,frequency .... 등등. 어떤 관련인지... 너무 쓸데없나? DELME
// TMP; CHK; Compiled at 2020-10-25
// 별로 중요하거나 엄밀한 내용은 아닌 듯, 나중에 삭제가능. 이걸 정리하려면 유사벡터=준벡터=pseudovector 등등 더 익혀야 하는게 많음.
4. Dimensionless ¶
번역어는 무엇인가? 무차원이 많이 나오는데 '1차원'도 가능? or 불가능? or 가능하지만 혼동을 주는 표현?
상수와 밀접.
1(하나,one), 자연로그의_밑,e, 원주율,pi(길이÷길이), 아보가드로수,Avogadro_constant 등 상수,constant는 모두 dimensionless.
1(하나,one), 자연로그의_밑,e, 원주율,pi(길이÷길이), 아보가드로수,Avogadro_constant 등 상수,constant는 모두 dimensionless.
2020-10-20 현재 이 위키에 언급된 것은
비중,specific_gravity (밀도/밀도)
유전상수,dielectric_constant (유전율/유전율)
라디안,radian (길이/길이) // curr at 각,angle#s-4
레이놀즈_수,Reynolds_number
수소이온농도지수,pH?
변형,strain (길이/길이)
비중,specific_gravity (밀도/밀도)
유전상수,dielectric_constant (유전율/유전율)
라디안,radian (길이/길이) // curr at 각,angle#s-4
레이놀즈_수,Reynolds_number
수소이온농도지수,pH?
변형,strain (길이/길이)
dimensionless quantity는 차원이 1이라고 한다. 0이 아님. (dimension less = 없다 = 0이다 이게 아님)
QQQ 이유나 설명? (1 이상의 자연수 n에 대해) n/n=1≠0 이라서? CHK
비,ratio 비율,rate 관련.단위,unit가 숫자 1?
그럼 conversion factor와 비슷?
통계학의 정규화,normalization와 비슷하다고?"Normalization (statistics) and standardized moment, the analogous concepts in statistics"
}5. 영차원 zero_dimension ¶
tbw 위 dimensionless 와 비교.
tbw 일차원 one_dimension ? 과 비교.
tbw 일차원 one_dimension ? 과 비교.
"zero-dimensional topological space (or nildimensional space) is..."
https://planetmath.org/zerodimensional9. 무한차원 (삭제무방) ¶
무한차원,infinite_dimension
https://everything2.com/title/infinite dimensions (깊은 수학 얘기는 없음)
Sub:
 무한차원
무한차원
 무한차원
무한차원
https://everything2.com/title/infinite dimensions (깊은 수학 얘기는 없음)
Sub:
무한차원벡터
무한차원벡터공간 - 벡터공간,vector_space#s-10
무한차원벡터함수 Infinite–dimensional_vector_function - 벡터함수,vector_function
Infinite–dimensional_vector_function - 벡터함수,vector_function
무한차원공간 infinite dimensional space무한차원벡터함수
10. 위상적 차원 topological dimension, 르베그 차원 Lebesgue dimension, 르베그 덮개 차원 Lebesgue covering dimension ¶
위상차원?
aka covering dimension, Lebesgue covering dimension
aka covering dimension, Lebesgue covering dimension
https://mathworld.wolfram.com/LebesgueCoveringDimension.html
https://encyclopediaofmath.org/wiki/Lebesgue_dimension
11. 크룰 차원 Krull dimension ¶
크룰_차원 Krull_dimension
가환대수,commutative_algebra에서, 가환환,commutative_ring 에 대한 차원?
소아이디얼,prime_ideal로 이루어진 진부분집합,proper_subsets들의 사슬,chain들의 크기의 상한,supremum. (wpko)
https://mathworld.wolfram.com/KrullDimension.html
 Krull_dimension
Krull_dimension
 크룰_차원
크룰_차원
가환대수,commutative_algebra에서, 가환환,commutative_ring 에 대한 차원?
소아이디얼,prime_ideal로 이루어진 진부분집합,proper_subsets들의 사슬,chain들의 크기의 상한,supremum. (wpko)
https://mathworld.wolfram.com/KrullDimension.html
14. Minkowski dimension ¶
민코프스키 차원
물리 관련?
물리 관련?
아닌듯? 그건 민코프스키_공간 or 시공간, Minkowski_space or Minkowski_spacetime, rel. 시공간,spacetime, see  Minkowski_space.
Minkowski_space.
같은 Hermann_Minkowski 의 업적은 맞는 것 같은데
같은 Hermann_Minkowski 의 업적은 맞는 것 같은데
이것은 (정수가 아닐 수 있는) 프랙탈차원,fractal_dimension. { https://foldoc.org/fractal dimension https://mathworld.wolfram.com/FractalDimension.html }
corresp. ko interwiki:
https://mathworld.wolfram.com/Minkowski-BouligandDimension.html
16. dimensionality ¶
뭐라고 번역해야? '차원, 차원 가능성, 차원수, 차원의 수' 등이 나오긴 하는데.
https://everything2.com/title/dimensionality
 dimensionality - 두번째 뜻은 명백히 '차원수'.
dimensionality - 두번째 뜻은 명백히 '차원수'.
https://everything2.com/title/dimensionality
2023-03-04 그냥 명사형은 -성 suffix를 붙이는 내 습관대로 '차원성'은 어떨까.. 그냥 차원으로 하면 pagename 여기랑 겹치기도 하고.
2024-04-13 차원수,dimensionality가 최선일 듯? + Sub 차원수저주,dimensionality_curse?
2024-04-13 차원수,dimensionality가 최선일 듯? + Sub 차원수저주,dimensionality_curse?
16.1. curse of dimensionality ¶
Richard_Bellman이 명명.
// tmp excerpt from 마스터 알고리즘
의사결정트리(decision_tree?)역시 차원의 저주에서 벗어나지 못한다. 예를 들어 학습하고자 하는 개념이 구,sphere라고 하자. 구 내부의 점들은 양이고 밖의 점들은 음이다. 의사결정트리는 구가 들어가는 가장 작은 정육면체,cube에 구를 근사,approximation시킬 수 있다. 완벽하지는 않지만 너무 나쁜 근사도 아니다. 정육면체의 구석들만 잘못 분류,classification한 셈이다. 하지만 고차원에서는 초정육면체(초입방체,hypercube)의 거의 모든 체적(부피,volume)이 초구,hypersphere 밖에 있다. 올바르게 양으로 분류한 사례에 비하여 틀리게 양으로 분류한 사례가 훨씬 더 많기 때문에 정확도,accuracy는 급락하고 만다.
사실 어떤 ML도 차원의 저주에서 벗어나지 못한다. 차원의 저주는 ML에서 과적합,overfitting 문제에 이어 두 번째로 가장 나쁜 골칫거리다. '차원의 저주'는 Richard Bellman이 1950년대에 만든 용어다. 그는 3차원에서 잘 작동한 제어 알고리즘control algorithm이 로봇 팔의 모든 관절이나 화학 공장의 모든 조절 손잡이를 제어하기 원할 때처럼 더 높은 차원의 공간에서는 절망스러울 정도로 비효율적이 되는 것을 발견했다. ... (그래서 대책은 관련 없는 차원들을 없애는 것.) .... 방의 천장이 높지만 데이터의 위치는 카펫에 앉은 얇은 먼지 층처럼 모두 바닥에 가까운 경우도 있다. 이것은 운이 좋은 경우다. 3차원 문제처럼 보이지만 사실상 2차원 문제에 더 가깝기 때문이다. 자연이 이미 우리를 위해 높이를 줄였기 때문에 우리가 높이를 줄일 필요가 없다. 데이터,data가 균일하게 (초)공간에 퍼지지 않은 이런 '비균일성의 축복'blessing of nonuniformity이 종종 곤경을 면하게 해 준다. ....
의사결정트리(decision_tree?)역시 차원의 저주에서 벗어나지 못한다. 예를 들어 학습하고자 하는 개념이 구,sphere라고 하자. 구 내부의 점들은 양이고 밖의 점들은 음이다. 의사결정트리는 구가 들어가는 가장 작은 정육면체,cube에 구를 근사,approximation시킬 수 있다. 완벽하지는 않지만 너무 나쁜 근사도 아니다. 정육면체의 구석들만 잘못 분류,classification한 셈이다. 하지만 고차원에서는 초정육면체(초입방체,hypercube)의 거의 모든 체적(부피,volume)이 초구,hypersphere 밖에 있다. 올바르게 양으로 분류한 사례에 비하여 틀리게 양으로 분류한 사례가 훨씬 더 많기 때문에 정확도,accuracy는 급락하고 만다.
사실 어떤 ML도 차원의 저주에서 벗어나지 못한다. 차원의 저주는 ML에서 과적합,overfitting 문제에 이어 두 번째로 가장 나쁜 골칫거리다. '차원의 저주'는 Richard Bellman이 1950년대에 만든 용어다. 그는 3차원에서 잘 작동한 제어 알고리즘control algorithm이 로봇 팔의 모든 관절이나 화학 공장의 모든 조절 손잡이를 제어하기 원할 때처럼 더 높은 차원의 공간에서는 절망스러울 정도로 비효율적이 되는 것을 발견했다. ... (그래서 대책은 관련 없는 차원들을 없애는 것.) .... 방의 천장이 높지만 데이터의 위치는 카펫에 앉은 얇은 먼지 층처럼 모두 바닥에 가까운 경우도 있다. 이것은 운이 좋은 경우다. 3차원 문제처럼 보이지만 사실상 2차원 문제에 더 가깝기 때문이다. 자연이 이미 우리를 위해 높이를 줄였기 때문에 우리가 높이를 줄일 필요가 없다. 데이터,data가 균일하게 (초)공간에 퍼지지 않은 이런 '비균일성의 축복'blessing of nonuniformity이 종종 곤경을 면하게 해 준다. ....
Twins
 curse_of_dimensionality
curse_of_dimensionality
 차원의_저주 //2022-02-02 현재 내용 한줄
차원의_저주 //2022-02-02 현재 내용 한줄
 Curse_of_dimensionality
Curse_of_dimensionality
https://everything2.com/title/curse of dimensionality
https://everything2.com/title/curse of dimensionality
17. dimension reduction / dimensionality reduction ¶
dimension_reduction AKA dimensionality_reduction
ML쪽. 번역어 후보: 차원감소 차원축소 차원줄이기 ...?
ML쪽. 번역어 후보: 차원감소 차원축소 차원줄이기 ...?
bmks ko
{
Machine Learning 스터디 (16) Dimensionality Reduction (PCA, LDA)
http://sanghyukchun.github.io/72/ (2015)
}
{
Machine Learning 스터디 (16) Dimensionality Reduction (PCA, LDA)
http://sanghyukchun.github.io/72/ (2015)
}
https://developers.google.com/machine-learning/glossary?hl=ko#dimension-reduction
물리학에서도 비슷한 용어 있음.
참고로 wpen은 이렇게 나눔.
manifold_learning
참고로 wpen은 이렇게 나눔.
dimensionality reduction, dimension reduction - ML쪽 용어
dimensional reduction - 물리 쪽 용어 (설명은 차원_축소_(물리학) 참조)
차원_축소_(물리학) 참조)
Reldimensional reduction - 물리 쪽 용어 (설명은
manifold_learning
21. Bmks en ¶
https://polytope.miraheze.org/wiki/Introduction_to_higher_dimensions From Polytope Wiki
https://everything2.com/title/Fourth dimension
https://everything2.com/title/Fifth dimension
https://everything2.com/title/Fourth dimension
https://everything2.com/title/Fifth dimension
Related:
자유도,degree_of_freedom
표준기저,standard_basis curr. see 기저,basis
물리의 시공간,spacetime - 3+1차원
{
공간,space 3차원 + 시간,time 1차원
 Spacetime
Spacetime
 시공간
시공간
}
자유도,degree_of_freedom
표준기저,standard_basis curr. see 기저,basis
cardinality of a basis -> Hamel dimension or algebraic dimension
벡터공간,vector_space물리의 시공간,spacetime - 3+1차원
{
공간,space 3차원 + 시간,time 1차원
}
Maybe related?? Compare?
n-튜플,tuple의 n?
arity 항수 애리티 애러티 (curr see 항수_(수학)
항수_(수학)  Arity)
Arity)
n-튜플,tuple의 n?
arity 항수 애리티 애러티 (curr see
이건
축,axis과 분명 관련있을텐데 어떻게 관련된것인지 tbw함수,function가 취하는 parameter/argument의 수.
연산자,operator가 취하는 operand의 수.
트리,tree의 어떤 노드가 가질 수 있는 최대 child 노드 수. (![[https]](/123/imgs/https.png) src)
src)
함수,function가 정의역,domain에서 취하는 독립변수의 수?
https://proofwiki.org/wiki/Definition:Operation/Arity - 연산,operation의 arity연산자,operator가 취하는 operand의 수.
트리,tree의 어떤 노드가 가질 수 있는 최대 child 노드 수. (
![[https]](/123/imgs/https.png) src)
src)함수,function가 정의역,domain에서 취하는 독립변수의 수?
Twins:
 Dimension
Dimension
![[https]](/123/imgs/https.png) 수학백과: 차원
수학백과: 차원
{ mentions:
벡터공간,vector_space의 차원
다양체의 차원
위상공간,topological_space의 차원 - 르베그_차원,Lebesgue_dimension or 덮개차원,covering_dimension
Hausdorff_dimension or fractal_dimension
Krull_dimension
}
https://mathworld.wolfram.com/Dimension.html
https://encyclopediaofmath.org/wiki/Dimension
https://encyclopediaofmath.org/wiki/Dimension_theory
https://polytope.miraheze.org/wiki/Dimension
https://planetmath.org/dimension
![[https]](/123/imgs/https.png) 수학백과: 차원
수학백과: 차원{ mentions:
벡터공간,vector_space의 차원
다양체의 차원
위상공간,topological_space의 차원 - 르베그_차원,Lebesgue_dimension or 덮개차원,covering_dimension
Hausdorff_dimension or fractal_dimension
Krull_dimension
}
https://mathworld.wolfram.com/Dimension.html
https://encyclopediaofmath.org/wiki/Dimension
https://encyclopediaofmath.org/wiki/Dimension_theory
https://polytope.miraheze.org/wiki/Dimension
https://planetmath.org/dimension
Up:


![[http]](/123/imgs/http.png)