접벡터,tangent_vector

접벡터 or 접선벡터

$\vec{r}(t)$ 가 parametric smooth curve일 때, // 매끄러움,smoothness 곡선,curve 매끄러운곡선,smooth_curve
tangent vector는:
$\vec{r}{}'(t)$
unit tangent vector는: (단위접벡터,unit_tangent_vector)
$\vec{T}(t)=\frac{\vec{r}{}'(t)}{|\vec{r}{}'(t)|}$

Compare: (tangent 시리즈)
접선,tangent_line과 유사? (curr. goto there)
접평면,tangent_plane?



mathworld는 반지름벡터,radius_vector를 먼저 정의
-> 반지름벡터는 위치벡터,position_vector와 동의어

rel, mklink
곡선,curve esp 공간곡선,space_curve(curr see 벡터함수,vector_function#s-7)

[edit]

Bazett

곡선 위의 한 점의 위치벡터,position_vector $\vec{r}(t)$ 가정.
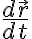$\frac{d\vec{r}}{dt}$ 를 어떻게 구할 것인가? 우선
$\frac{\Delta\vec{r}}{\Delta t}=\frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t}$
여기서 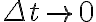$\Delta t\to 0$ 극한을 생각하면
$\frac{d\vec{r}}{dt}=\lim_{\Delta t\to 0}\frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t}$
그리고 $\vec{r}(t)=f(t)i+g(t)j+h(t)k$ 라면
$\vec{r}(t+\Delta t)-\vec{r}(t)$
$=[f(t+\Delta t)i+g(t+\Delta t)j+h(t+\Delta t)k]-[f(t)i+g(t)j+h(t)k]$
$=[f(t+\Delta t)-f(t)]i+[g(t+\Delta t)-g(t)]j+[h(t+\Delta t)-h(t)]k$
따라서 구하고자 하는 식은
$\lim_{\Delta t\to 0}\frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t}$
$=\lim_{\Delta t\to 0}\left(\frac{f(t+\Delta t)-f(t)}{\Delta t}\right)i+\lim_{\Delta t\to 0}(...)j+\lim_{\Delta t\to 0}(...)k$
$=\frac{df}{dt}i+\frac{dg}{dt}j+\frac{dh}{dt}k$

Leibniz 표기법:
$\frac{d\vec{r}}{dt}=\frac{df}{dt}\hat{\rm i}+\frac{dg}{dt}\hat{\rm j}+\frac{dh}{dt}\hat{\rm k}$
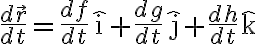
Lagrange 표기법:
$\vec{r}{}'(t)=f'(t)\hat{\rm i}+g'(t)\hat{\rm j}+h'(t)\hat{\rm k}$

(https://youtu.be/40r56pX4mqA 3:30)


할벡터? 할선벡터? secant_vector
{
secant vector:
$\vec{r}(t+h)-\vec{r}(t)$
그리고 이것도? (크기는 무관?)
$\frac{\vec{r}(t+h)-\vec{r}(t)}{h}$

tangent vector: (접벡터,tangent_vector)
$\lim_{h\to 0} \frac{\vec{r}(t+h)-\vec{r}(t)}{h} = \vec{r}'(t)$

unit tangent vector: (단위접벡터,unit_tangent_vector)
$\frac{\vec{r}{}'(t)}{\left|\vec{r}{}'(t)\right|}=\vec{T}(t)$

(Stewart)

}