접평면,tangent_plane

$z-z_0=\left({\partial f \over \partial x}\right)(x-x_0)+\left(\frac{\partial f}{\partial y}\right)(y-y_0)$

(MathWorld) 곡면,surface 함수 $z=f(x,y)$ 위의 임의의 점 $(x_0,y_0)$ 가 있으면, 곡면은 $(x_0,y_0)$ 에서 다음 방정식으로 주어지는 곡면과? 수직이 아닌(nonvertical) 접평면 하나를 가진다.

$z=f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)$

$f$ 가 연속인 편도함수(=편미분,partial_derivative)를 갖는다고 가정하자.
점 $P(x_0,y_0,z_0)$ 에서 곡면,surface $z=f(x,y)$ 에 대한 접평면의 방정식은 다음과 같다.

$z-z_0=f_x(x_0,y_0)(x-x_0) + f_y(x_0,y_0)(y-y_0)$

다음 접선,tangent_line의 방정식과 비슷함에 유의.

$y-y_0=f'(x_0)(x-x_0)$

(이어서 접평면근사,tangent_plane_approximation, curr at 선형근사,linear_approximation#multivariable case - 설명함.)
점 $(a,b,f(a,b))$ 에서 이변수함수 $f$ 의 그래프에 대한 접평면의 방정식은 다음과 같다.

$z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)$

(Stewart 8e ko p769-771)

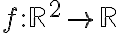Let $f:\mathbb{R}^2\to\mathbb{R}$ be differentiable at $\vec{x_0}=(x_0,y_0).$
The plane in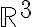 $\mathbb{R}^3$ defined by the equation

$z=f(x_0,y_0)+\left[\frac{\partial f}{\partial x}(x_0,y_0)\right](x-x_0)+\left[\frac{\partial f}{\partial y}(x_0,y_0)\right](y-y_0)$

is called the tangent plane of the graph of $f$ at the point $(x_0,y_0,f(x_0,y_0)).$

(Vector Calculus 6e (2012))

QQQ '접촉평면'은 어떻게 다른 것?

접평면 접촉평면

tangent.plane osculating.plane difference

접촉평면,osculating_plane

QQQ 혹시 매끄러운 곡면,surface 위의 한 점,point에서만 정의되나? cusp, singularity 이런데선 당연히 안 될 것 같은데. CHK

$z_0=f(x_0,y_0)$ 를 지나고 $z=f(x,y)$ 를 스치는 평면,plane은? - CHK

전제: $P_0(x_0,y_0,z_0),\quad P(x,y,z)$
평면의 방정식:

$\vec{n}\cdot\vec{P_0P}=0$
$a(x-x_0)+b(y-y_0)=c(z-z_0)=0$

이하 선형근사,linear_approximation 관련 얘기가 나오는데 안 적음..
관련된것임
찾아보니 전미분도 관련.

[https]

Related:
아마 분명 관련, 관계 TBW
기울기,gradient
기울기벡터,gradient_vector
방향도함수,directional_derivative

Twins:

[https]

수학백과: 접평면
https://mathworld.wolfram.com/TangentPlane.html (short, 위에 번역)
https://everything2.com/title/Tangent plane

AKA tangential plane

Compare:

// 다음 4개는 이름의 차원,dimension순인데 구체적으로 어떤 관계인지? tbw
접점,tangent_point - 이건 아래 선/평면에 비해 잘 안 쓰이는 표현...? tangent.point .... 접점 접점

이건 분명 logical_conjunction, AND 와도 밀접한데... chk later
// kms 접점 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=접점
// QQQ kms osculat => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=osculat ...을 보면 osculating_point의 번역은 '접촉점' ??? TBD and MKLINK

접선,tangent_line
접평면,tangent_plane
접공간,tangent_space - 접다발의 올,fiber chk

접벡터,tangent_vector
접다발,tangent_bundle

Up: 탄젠트,tangent 평면,plane