Difference between r1.17 and the current

@@ -6,6 +6,12 @@

$f(a)$ 와 $f(b)$ 사이의 임의의 실수 $k$ 에 대하여
$f(c)=k$
인 c가 a와 b 사이에 적어도 하나 존재한다.

----

$f:\,[a,b]$ 에서 연속인 함수이고

$f(a)\ne f(b)$ 일 때

$f(a)<N<f(b)$ 또는 $f(b)<N<f(a)$ 인 임의의 $N$ 에 대하여

$\exists c\in[a,b]$ such that $f(c)=N.$

## 단대 김도형 일반수학1 2. 1:30m http://www.kocw.net/home/search/kemView.do?kemId=1177885

----
Let $f:[a,b]\mapsto\mathbb{R}$ be a continuous function.
Then for all $y\in\mathbb{R}$ between $f(a)$ and $f(b)$

@@ -14,13 +20,26 @@

Suppose $f$ is continuous on a closed interval $[a,b]$ .
$\forall k \textrm{ between } f(a) \textrm{ and } f(b)$
$\exists c \in [a,b] \,\textrm{ such that }\, f(c)=k$

----

관련: [[연속성,continuity]]
기타 필요한것... [[유계,bounded]] [[상한,supremum]] [[상계,upper_bound]]

증명은 [[실수,real_number]] [[완비성,completeness]]에 의존하므로 더 advanced texts에. (Thomas)

= 중간값 성질 intermediate value property =

중간값성질 사이값성질 intermediate value property

$f$ 는 폐구간 $[a,b]$ 상에서 연속함수이고, $y_0$ 는 $f(a)$ 와 $f(b)$ 사이의 임의의 수이면,
$y_0=f(c)$ 를 만족하는 수 $c\in[a,b]$ 가 존재한다.

----

[[닫힌구간,closed_interval]] $[a,b]$ 에서 [[연속성,continuity|연속]]인 [[함수,function]] $y=f(x)$ 는 $f(a)$ 와 $f(b)$ 사이의 모든 값을 가진다.

다른 말로 하면, $y_0$ 가 $f(a)$ 와 $f(b)$ 사이의 임의의 값일 때, 어떤 $c\in[a,b]$ 에 대해 $y_0=f(c)$ 이다.

(Thomas)

// intermediate_value_property Google:intermediate.value.property Google:중간값+성질

[[성질,property]]

= tmp links =
고등학교 과정으로 증명하기

@@ -47,6 +66,9 @@

Up: [[정리,theorem]]
}

비교:

[[평균값정리,mean_value_theorem,MVT]]

----
Twins:

@@ -58,6 +80,8 @@

https://everything2.com/title/Intermediate+Value+Theorem
https://artofproblemsolving.com/wiki/index.php/Intermediate_Value_Theorem
https://brilliant.org/wiki/intermediate-value-theorem/

https://mathworld.wolfram.com/IntermediateValueTheorem.html

....
Google:중간값.정리

@@ -65,5 +89,4 @@

Up: [[미적분,calculus]]
[[real_analysis]]
[[정리,theorem]]

$f$ 가 $[a,b]$ 에서 정의된 함수이며 $W$ 는 $f(a)$ 와 $f(b)$ 사이의 값이라고 하자.
$f$ 가 $[a,b]$ 에서 연속일 때,
$f(c)=W$ 인 $c$ 가 $a$ 와 $b$ 사이에 존재한다.

함수 $f(x)$ 가 폐구간 $[a,\,b]$ 에서 연속이고 $f(a)\neq f(b)$ 일 때,
$f(a)$ 와 $f(b)$ 사이의 임의의 실수 $k$ 에 대하여

$f(c)=k$

인 c가 a와 b 사이에 적어도 하나 존재한다.

$f:\,[a,b]$ 에서 연속인 함수이고
$f(a)\ne f(b)$ 일 때
$f(a)<N<f(b)$ 또는 $f(b)<N<f(a)$ 인 임의의 $N$ 에 대하여
$\exists c\in[a,b]$ such that $f(c)=N.$

Let $f:[a,b]\mapsto\mathbb{R}$ be a continuous function.
Then for all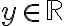 $y\in\mathbb{R}$ between $f(a)$ and $f(b)$
there exists a value $x\in[a,b]$ such that $f(x)=y$ .

Suppose $f$ is continuous on a closed interval $[a,b]$ .
$\forall k \textrm{ between } f(a) \textrm{ and } f(b)$
$\exists c \in [a,b] \,\textrm{ such that }\, f(c)=k$

관련: 연속성,continuity
기타 필요한것... 유계,bounded 상한,supremum 상계,upper_bound

증명은 실수,real_number 완비성,completeness에 의존하므로 더 advanced texts에. (Thomas)

[edit]

중간값 성질 intermediate value property ¶

중간값성질 사이값성질 intermediate value property

$f$ 는 폐구간 $[a,b]$ 상에서 연속함수이고, $y_0$ 는 $f(a)$ 와 $f(b)$ 사이의 임의의 수이면,
$y_0=f(c)$ 를 만족하는 수 $c\in[a,b]$ 가 존재한다.

닫힌구간,closed_interval $[a,b]$ 에서 연속인 함수,function $y=f(x)$ 는 $f(a)$ 와 $f(b)$ 사이의 모든 값을 가진다.
다른 말로 하면,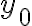 $y_0$ 가 $f(a)$ 와 $f(b)$ 사이의 임의의 값일 때, 어떤 $c\in[a,b]$ 에 대해 $y_0=f(c)$ 이다.
(Thomas)

// intermediate_value_property