일단은 평면 극좌표계를 다룸
극좌표,polar_coordinate - merge?
평면,plane 위 점,point의 위치,position를,
- 원점,origin으로부터의 거리,distance와
- 원점 기준 방향,direction(rel. 시초선과의 각,angle)
미소 ¶
극좌표계 ) 에서,
에서,
지름 방향의 미소 변화는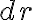 이고, 지름이
이고, 지름이  일 때 중심각 변화
일 때 중심각 변화 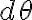 인 호의 길이는
인 호의 길이는  이므로
이므로
미소면적은
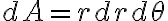
이것을 확장하면 원통좌표계 ) 에선
에선
지름 방향으로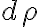 이고, 지름이
이고, 지름이 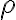 일 때 중심각 변화
일 때 중심각 변화 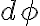 인 호의 길이는
인 호의 길이는 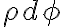 이므로
이므로
xy평면 위의 미소면적은
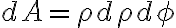
따라서 미소부피는 여기에 높이 방향의 미소 변화량 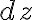 를 곱한
를 곱한
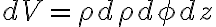
참고로 원통 겉면의 면적소는 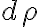 를 빼면 되므로
를 빼면 되므로
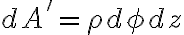
지름 방향의 미소 변화는
미소면적은
지름 방향으로
xy평면 위의 미소면적은
극좌표계에서 원의 표현 ¶
이하 내용 와선 or spiral 으로 분리? ¶
그럼 pagename TBD.
kms spiral => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral
kms 와선 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=와선 (2022-12-24에 none.)
kms spiral => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral
kms 와선 => https://www.kms.or.kr/mathdict/list.html?key=kname&keyword=와선 (2022-12-24에 none.)
로그 와선 logarithmic spiral ¶
식
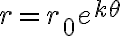
로 표현. 여기서 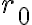 와
와  는 0이 아닌 상수.
는 0이 아닌 상수.
로그 와선은 한바퀴씩 돌 때마다 원점에서의 거리,distance가 일정한 비율로 나타난다. 또 원점을 지나는 직선과 와선의 각 점에서의 접선,tangent_line은 항상 일정한 각,angle을 이루고 있어서, 이 곡선을 등각 와선(equi-angular spiral)이라고도 부른다.
(김홍종)
로그 와선은 한바퀴씩 돌 때마다 원점에서의 거리,distance가 일정한 비율로 나타난다. 또 원점을 지나는 직선과 와선의 각 점에서의 접선,tangent_line은 항상 일정한 각,angle을 이루고 있어서, 이 곡선을 등각 와선(equi-angular spiral)이라고도 부른다.
(김홍종)
gnuplot ¶
gnuplot에서 극좌표계 모드로 변환하기
![[https]](/123/imgs/https.png) https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
set polar
직교 좌표계 모드로 돌아가기set nopolar
(from ![[https]](/123/imgs/https.png) https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
https://wiki.kldp.org/KoreanDoc/html/GnuPlot-KLDP/polar.html)
