기호: 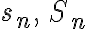
Partial sums:
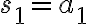
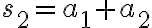
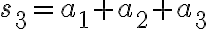
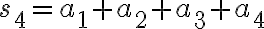
and, in general,
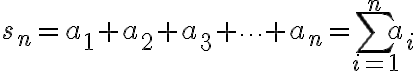
and, in general,
급수,series
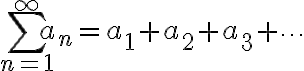
에서  번째 부분합
번째 부분합 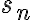 은
은
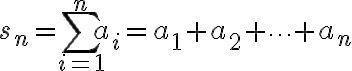
이며, 수열,sequence 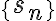 이 수렴하고 극한
이 수렴하고 극한 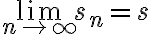 가 실수,real_number로 존재하면, 급수,series
가 실수,real_number로 존재하면, 급수,series 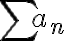 은 수렴,convergence한다고 하며
은 수렴,convergence한다고 하며
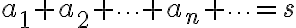 또는
또는
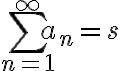
로 쓴다. 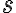 가 급수의 합,sum이다.
가 급수의 합,sum이다.
수열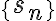 이 발산하면, 급수도 발산,divergence한다.
이 발산하면, 급수도 발산,divergence한다.
수열
(Stewart)
무한급수,infinite_series의 값(합,sum)을 구할 때 식을 바로 나타내기 어려우므로 부분합을 식으로 나타낸 다음 부분합 식에서 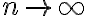 극한,limit을 구하는 방식이 많이 보임.
극한,limit을 구하는 방식이 많이 보임.
tmp (적절한 곳으로 이동 무방)
{
정리
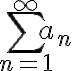 이 수렴하면,
이 수렴하면, 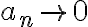 이다.
이다.
발산을 알아보는 일반항 판정법
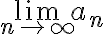 이 존재하지 않거나
이 존재하지 않거나 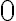 이 아닌 다른 값이면,
이 아닌 다른 값이면, 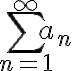 은 발산한다.
은 발산한다.
// rel. 판정법,test#s-1.1 발산,divergence 수렴,convergence 수렴판정법,convergence_test
(Thomas 13e ko 8.2 무한급수 p472)
}
{
정리
(Thomas 13e ko 8.2 무한급수 p472)
}

