공분산,covariance (rev. 1.36)
분산과는 달리 0 또는 음수일 수 있음.
// 데과기 Week 9-1 p7
Covariance:
![$\text{Cov}[X,Y]$](/123/cgi-bin/mimetex.cgi?\Large \text{Cov}[X,Y] "$\text{Cov}[X,Y]$")
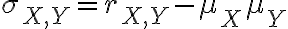
- One simple value to represent the relation between two random variables
- Represent how two random variables vary together
성질들:
![$\text{Cov}[aX,bY]=ab\text{Cov}[X,Y]$](/123/cgi-bin/mimetex.cgi?\Large \text{Cov}[aX,bY]=ab\text{Cov}[X,Y] "$\text{Cov}[aX,bY]=ab\text{Cov}[X,Y]$")
... // 스케일 된 확률변수의 경우.
![$\text{Cov}[X,X]=\text{Var}[X]$](/123/cgi-bin/mimetex.cgi?\Large \text{Cov}[X,X]=\text{Var}[X] "$\text{Cov}[X,X]=\text{Var}[X]$")
이 다음에 다루는 것은 상관계수,correlation_coefficient.
저것은 공분산을 분산,variance으로 scale한 것. (Covariance scaled by variance)
저것의 값은 -1에서 1 사이. (Strictly between -1 and 1)
저것의 식은
![$\rho_{X,Y}=\frac{\text{Cov}[X,Y]}{\sqrt{\text{Var}[X]\text{Var}[Y]}}$](/123/cgi-bin/mimetex.cgi?\Large \rho_{X,Y}=\frac{\text{Cov}[X,Y]}{\sqrt{\text{Var}[X]\text{Var}[Y]}} "$\rho_{X,Y}=\frac{\text{Cov}[X,Y]}{\sqrt{\text{Var}[X]\text{Var}[Y]}}$")
저것은 공분산을 분산,variance으로 scale한 것. (Covariance scaled by variance)
저것의 값은 -1에서 1 사이. (Strictly between -1 and 1)
저것의 식은
확률변수 X, Y에 대해
=\mu_X "$E(X)=\mu_X$")
와 =\mu_Y "$E(Y)=\mu_Y$")
가 존재하면
X와 Y의 공분산은
![$\mathrm{Cov}(X,Y):=E[(X-\mu_X)(Y-\mu_Y)]$](/123/cgi-bin/mimetex.cgi?\Large \mathrm{Cov}(X,Y):=E[(X-\mu_X)(Y-\mu_Y)] "$\mathrm{Cov}(X,Y):=E[(X-\mu_X)(Y-\mu_Y)]$")
=\frac1N\sum(x_i-\bar{x})(y_j-\bar{y}) "$\textrm{Cov}(x,y)=\frac1N\sum(x_i-\bar{x})(y_j-\bar{y})$")
공분산의 정의
x와 y의 공분산을 cxy라 하면
(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} "$c_{xy}=\frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n}$")
즉, 분산이 xx(x2)이라면 공분산은 그 자리에 xy분산의 ^2 "$(x_i-\bar{x})^2$")
자리에 공분산은 (y_i-\bar{y}) "$(x_i-\bar{x})(y_i-\bar{y})$")
가 오는 그런 꼴
(통계가 빨라지는 수학력 책에서 인용)
두 확률변수의 관계를 보여주는 값.
확률변수 X, Y가 같이 변하는 정도를 나타내는 값.
확률변수 X, Y에 대해 X가 변할 때 Y가 변하는 정도를 나타내는 값.
(Y-\mu_y) "$(X-\mu_x)(Y-\mu_y)$")
의 평균,mean,average으로 정의.
![$\mathrm{Cov}(X,Y)=E[(X-\mu_x)(Y-\mu_y)]$](/123/cgi-bin/mimetex.cgi?\Large \mathrm{Cov}(X,Y)=E[(X-\mu_x)(Y-\mu_y)] "$\mathrm{Cov}(X,Y)=E[(X-\mu_x)(Y-\mu_y)]$")
여기서
즉 편차의 곱의 평균으로 정의.
확률변수 X, Y가 같이 변하는 정도를 나타내는 값.
확률변수 X, Y에 대해 X가 변할 때 Y가 변하는 정도를 나타내는 값.
즉 편차의 곱의 평균으로 정의.
이산확률변수,discrete_random_variable의 공분산:
=\sum_x \sum_y (x-\mu_x)(y-\mu_y)\cdot f(x,y) "$\mathrm{Cov}(X,Y)=\sum_x \sum_y (x-\mu_x)(y-\mu_y)\cdot f(x,y)$")
연속확률변수,continuous_random_variable의 공분산:
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} (x-\mu_x)(y-\mu_y)\cdot f(x,y) dxdy "$\mathrm{Cov}(X,Y)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} (x-\mu_x)(y-\mu_y)\cdot f(x,y) dxdy$")
기타 다음 식도 성립
X, Y가 서로 독립이면 E(XY)=E(X)E(Y)이다. 이 때,
Cov(X,Y)=E(XY)-E(X)E(Y)=E(X)E(Y)-E(X)E(Y)=0
공분산은 X가 변할 때 Y가 변하는 정도와 관련되는데, X와 Y가 독립이면 값이 0이 나옴을 볼 수 있다.
X, Y가 서로 독립이면 E(XY)=E(X)E(Y)이다. 이 때,
Cov(X,Y)=E(XY)-E(X)E(Y)=E(X)E(Y)-E(X)E(Y)=0
공분산은 X가 변할 때 Y가 변하는 정도와 관련되는데, X와 Y가 독립이면 값이 0이 나옴을 볼 수 있다.
Cov(aX, bY) = a b Cov(X, Y)
Cov(X+a, Y+b) = Cov(X, Y)
Cov(X, aX+b) = a Var(X)
Cov(aX+b, cX+d) = a c Var(X)
공분산의 단점은 '어느 정도' 연관되어 있는지 그 단위/스케일에 대한 것. 강도(strength)를 잘 보여주지 못함. 이것을 개선한 것이 상관계수,correlation_coefficient. (공분산을 표준편차의 곱으로 나눔)
3. 공분산(covariance)과 상관계수(correlation coefficient) ¶
전제:
=\mu_X,\;E(Y)=\mu_Y "$E(X)=\mu_X,\;E(Y)=\mu_Y$")
가 존재할 때
![$\operatorname{Cov}(X,Y)=E\left[(X-\mu_X)(Y-\mu_Y)\right]$](/123/cgi-bin/mimetex.cgi?\Large \operatorname{Cov}(X,Y)=E\left[(X-\mu_X)(Y-\mu_Y)\right] "$\operatorname{Cov}(X,Y)=E\left[(X-\mu_X)(Y-\mu_Y)\right]$")
전제:
=\sigma_X^2 "${\rm Var}(X)=\sigma_X^2$")
과
=\sigma_Y^2 "${\rm Var}(Y)=\sigma_Y^2$")
가 각각 존재할 때 X와 Y의 상관계수는
=\rho_{XY}=\frac{{\rm Cov}(X,Y)}{\sqrt{{\rm Var}(X)}\sqrt{{\rm Var}(Y)}} "$\rho(X,Y)=\rho_{XY}=\frac{{\rm Cov}(X,Y)}{\sqrt{{\rm Var}(X)}\sqrt{{\rm Var}(Y)}}$")
Note:
=E(XY)-E(X)E(Y) "${\rm Cov}(X,Y)=E(XY)-E(X)E(Y)$")
from http://www.kocw.net/home/search/kemView.do?kemId=1162312 4장_확률변수와분포_분산
4. 공분산의 성질 ¶
Var(X) = Cov(X, X)
Cov(X, Y) = Cov(Y, X)
Var(X + Y) = Var(X) + Var(Y) + 2Cov(X, Y)
Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z)
Cov(X, Y) = Cov(Y, X)
Var(X + Y) = Var(X) + Var(Y) + 2Cov(X, Y)
Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z)
6. 웹페이지 요약 DELME later.. ¶
from 두산백과
from 수학백과
확률변수 X, Y의 기대값,expected_value을 각각 ,\,\mu_Y=E(Y) "$\mu_X=E(X),\,\mu_Y=E(Y)$")
라 하면 공분산은
=E((X-\mu_X)(Y-\mu_Y)) "$\mathrm{Cov}(X,Y)=E((X-\mu_X)(Y-\mu_Y))$")
-E(X)E(Y) "$=E(XY)-E(X)E(Y)$")
공분산=0이면, 상관없다(uncorrelated)
두 확률변수가 독립이면, 공분산은 0이다. 그러나 역은 일반적으로 참이 아니다.
공분산을 각 변수의 표준편차로 나누면 상관계수(Corr(X, Y))
=\frac{\mathrm{Cov}(X,Y)}{\sqrt{V(X)V(Y)}} "$\mathrm{Corr}(X,Y)=\frac{\mathrm{Cov}(X,Y)}{\sqrt{V(X)V(Y)}}$")
두 확률변수가 독립이면, 공분산은 0이다. 그러나 역은 일반적으로 참이 아니다.
공분산을 각 변수의 표준편차로 나누면 상관계수(Corr(X, Y))
7. 기타 ¶
PL에서 covariance (그리고 contravariance) 에 대해서는 여길 참조 - 
Covariance_and_contravariance_(computer_science)
Covariance_and_contravariance_(computer_science)
![[https]](/123/imgs/https.png)
