Difference between r1.4 and the current
@@ -22,10 +22,6 @@
$\text{V}[X']=\frac{1-p}{p^2}$독립적 베르누이 시행에서, $X'=X+1$ 은 처음 --성공하기 전까지-- 성공할 때 까지 시도한 횟수. (number of trials until the first success)
----
Source: Leon-Garcia Table 3.1
@@ -51,10 +47,14 @@
$p_X(k)=p(X=k)=(1-p)^{k-1}p,\;\;\;k=1,2,3,\ldots$Source: [[https://terms.naver.com/entry.naver?docId=3405096&cid=47324&categoryId=47324 수학백과: 베르누이 시행]] 3.2.
----
Related: [[기하분포,geometric_distribution]]
연속확률변수인 [[지수확률변수,exponential_random_variable]]와 밀접.
----
[[https://terms.naver.com/entry.naver?docId=3338153&cid=47324&categoryId=47324 수학백과: 기하변수]]
Up: [[이산확률변수,discrete_random_variable]]
성공 확률이 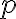 인 베르누이_시행,Bernoulli_trial에서 처음 성공이 일어날 때 까지 반복한 시행,trial 횟수를
인 베르누이_시행,Bernoulli_trial에서 처음 성공이 일어날 때 까지 반복한 시행,trial 횟수를  라 할 때,
라 할 때,
 를 성공 확률이
를 성공 확률이 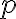 인 기하확률변수라 하고
인 기하확률변수라 하고
)
로 나타냄.
First Version ¶
독립적 베르누이_시행,Bernoulli_trial에서, X는 처음 성공하기 전까지 벌어진 실패의 횟수. (number of failures before the first success)
기하확률변수는 memoryless property(see 무기억성,memorylessness)를 가진 유일한 이산확률변수임.
기하확률변수는 memoryless property(see 무기억성,memorylessness)를 가진 유일한 이산확률변수임.
Second Version ¶
독립적 베르누이 시행에서, 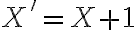 은 처음
은 처음 성공하기 전까지 성공할 때 까지 시도한 횟수. (number of trials until the first success)
Source: Leon-Garcia Table 3.1
성공 확률이 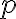 인 베르누이_시행,Bernoulli_trial을
인 베르누이_시행,Bernoulli_trial을
성공이 나올때까지 반복한 횟수를 라 하면,
라 하면,
 는 모수가
는 모수가 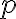 인 기하분포,geometric_distribution를 따른다고 한다.
인 기하분포,geometric_distribution를 따른다고 한다.
성공이 나올때까지 반복한 횟수를
기하분포를 따르는 확률변수,random_variable를 기하확률변수 또는 줄여서 기하변수라고 한다.
Source:
![[https]](/123/imgs/https.png) 수학백과: 베르누이 시행 3.2.
수학백과: 베르누이 시행 3.2.Related: 기하분포,geometric_distribution
연속확률변수인 지수확률변수,exponential_random_variable와 밀접.

