Difference between r1.47 and the current
@@ -13,49 +13,11 @@
모든 '''다항식'''의 [[정의역,domain]]은$\mathbb{R}=(-\infty,\infty)$
----
[[항,term]] 수가 하나인 다항식.
'''다항식,polynomial'''은, [[단항식,monomial]](들)의 [[합,sum]].
'''다항식''' 중에서, 더해지는 항(term)의 개수가 1이면 단항식. (이름과는 좀 맞지 않지만)
'''다항식''' 중에서, 더해지는 [[항,term]]의 개수가 1이면 단항식. (이름과는 좀 맞지 않지만) (i.e. 다항식은 항상 '많은 수의 항, 여러 개의 항'이 아님. 단항식도 다항식의 일종. 다항식의 특수한 경우(항이 한 개인 경우)가 단항식.)
----See also [[다항함수,polynomial_function]]
{다음과 같이 표현되는 함수 $P$ 를 '''다항함수'''라고 한다.
$P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_2x^2+a_1x+a_0$
@@ -83,7 +45,7 @@
----
선형대수적 관점에서, [* https://www.youtube.com/watch?v=TgKwz5Ikpc8 7:50]
space: all polynomials
[[공간,space]]: all polynomials
[[기저,basis]] functions:$b_0(x)=1$
$b_1(x)=x$
@@ -91,7 +53,7 @@
$b_3(x)=x^3$$\vdots$
그리고 이것들의 [[선형결합,linear_combination]]이 '''polynomial'''...
''QQQ 명칭이 [[기저함수]] ? Ndict:기저함수 ([[LCAO]]언급) Ggl:기저함수 WtEn:basis_function WpEn:basis_function ?
----Sub:
[[테일러_다항식,Taylor_polynomial]]
@@ -111,6 +73,11 @@
[[Jacobi_polynomial]] - 〃[[기약다항식,irreducible_polynomial]] - 〃
[[가약다항식,reducible_polynomial]] - 〃
[[다항식높이,polynomial_height]] (? tentative pagename) - w
https://mathworld.wolfram.com/PolynomialHeight.html
polynomial_factorization - [[인자분해,factorization]] w
= TBW - 용어/분류 임시 =
다항식의 용어들이나 분류 - 서술예정, 개요만 간략히 적어둠 (고급수학.pdf p35)
@@ -180,6 +147,12 @@
WpKo:호너의_방법[[WpEn:Horner's_method]]
다만 MW에서 쓰는 용어는 https://mathworld.wolfram.com/HornersRule.html 이다. https://mathworld.wolfram.com/HornersMethod.html 가 아니고.
''[[Date(2023-08-16T03:43:46)]]: found [[WtEn:Horner's_method]] & [[WtEn:Horner's_rule]]''
''is_a 다항식평가 polynomial_evaluation ? { Up: [[다항식,polynomial]] [[평가,evaluation]] }''
= w =
Sub:
[[매듭다항식,knot_polynomial]]
----
Twins:
@@ -190,7 +163,7 @@
Libre:다항식http://oeis.org/wiki/Polynomials
https://ncatlab.org/nlab/show/polynomial
Up: [[식,expression]]?
- 상수
은 다항식의 계수,coefficient이다.
일 때, 차수,degree는
이다. 다항식
의 차수가
인 것을 식으로 나타내면
이다.
다항식 중에서, 더해지는 항,term의 개수가 1이면 단항식. (이름과는 좀 맞지 않지만) (i.e. 다항식은 항상 '많은 수의 항, 여러 개의 항'이 아님. 단항식도 다항식의 일종. 다항식의 특수한 경우(항이 한 개인 경우)가 단항식.)
See also 다항함수,polynomial_function
{
다음과 같이 표현되는 함수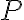 를 다항함수라고 한다.
를 다항함수라고 한다.
=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_2x^2+a_1x+a_0)
여기서  은 음이 아닌 정수이고
은 음이 아닌 정수이고
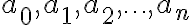 은 상수로서 다항함수의 계수,coefficient라 한다.
은 상수로서 다항함수의 계수,coefficient라 한다.
임의의 다항함수의 정의역은) 이다.
이다.
최고차항 계수가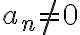 이면, 다항함수의 차수,degree는
이면, 다항함수의 차수,degree는  이다.
이다.
1차 다항함수는 일차함수(선형함수)
2차 다항함수는 이차함수,quadratic_function
3차 다항함수는 삼차함수,cubic_function
(Stewart 8e 번역서)
{
다음과 같이 표현되는 함수
임의의 다항함수의 정의역은
최고차항 계수가
1차 다항함수는 일차함수(선형함수)
2차 다항함수는 이차함수,quadratic_function
3차 다항함수는 삼차함수,cubic_function
(Stewart 8e 번역서)
선형대수적 관점에서, [1]
공간,space: all polynomials
기저,basis functions:
=1)
=x)
=x^2)
=x^3)
그리고 이것들의 선형결합,linear_combination이 polynomial...
''QQQ 명칭이 기저함수 ? 기저함수 (LCAO언급)
기저함수 (LCAO언급)  기저함수
기저함수  basis_function
basis_function  basis_function ?
basis_function ?
공간,space: all polynomials
기저,basis functions:
''QQQ 명칭이 기저함수 ?
Sub:
![[https]](/123/imgs/https.png) 수학백과: 최소다항식에는 다음 두 뜻이.
수학백과: 최소다항식에는 다음 두 뜻이.
![[https]](/123/imgs/https.png) 수학백과: 최소다항식(선형대수학)
수학백과: 최소다항식(선형대수학)
![[https]](/123/imgs/https.png) 수학백과: 최소다항식(체론)
수학백과: 최소다항식(체론)
}
테일러_다항식,Taylor_polynomial
특성다항식,characteristic_polynomial - 특성방정식,characteristic_equation의 LHS
직교다항식,orthogonal_polynomial - curr at 직교성,orthogonality
르장드르_다항식,Legendre_polynomial - writing
최소다항식,minimal_polynomial - writing
{특성다항식,characteristic_polynomial - 특성방정식,characteristic_equation의 LHS
직교다항식,orthogonal_polynomial - curr at 직교성,orthogonality
르장드르_다항식,Legendre_polynomial - writing
최소다항식,minimal_polynomial - writing
![[https]](/123/imgs/https.png) 수학백과: 최소다항식에는 다음 두 뜻이.
수학백과: 최소다항식에는 다음 두 뜻이.![[https]](/123/imgs/https.png) 수학백과: 최소다항식(선형대수학)
수학백과: 최소다항식(선형대수학)![[https]](/123/imgs/https.png) 수학백과: 최소다항식(체론)
수학백과: 최소다항식(체론)}
라그랑주_다항식,Lagrange_polynomial - writing ... rel. 보간,interpolation > 라그랑주_보간,Lagrange_interpolation
방데르몽드_다항식,Vandermonde_polynomial - 방데르몽드_행렬,Vandermonde_matrix의 행렬식,determinant. (curr see 행렬,matrix)
monic_polynomial - 최고차항 계수가 1인 다항식. 작성중.
Laguerre_polynomial - 작성중
Jacobi_polynomial - 〃
기약다항식,irreducible_polynomial - 〃
가약다항식,reducible_polynomial - 〃
다항식높이,polynomial_height (? tentative pagename) - w
polynomial_factorization - 인자분해,factorization w
방데르몽드_다항식,Vandermonde_polynomial - 방데르몽드_행렬,Vandermonde_matrix의 행렬식,determinant. (curr see 행렬,matrix)
monic_polynomial - 최고차항 계수가 1인 다항식. 작성중.
Laguerre_polynomial - 작성중
Jacobi_polynomial - 〃
기약다항식,irreducible_polynomial - 〃
가약다항식,reducible_polynomial - 〃
다항식높이,polynomial_height (? tentative pagename) - w
polynomial_factorization - 인자분해,factorization w
TBW - 용어/분류 임시 ¶
다항식의 용어들이나 분류 - 서술예정, 개요만 간략히 적어둠 (고급수학.pdf p35)
{
다항식
=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0)
where
 : 음이 아닌 정수,
: 음이 아닌 정수, 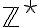
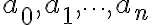 :
: 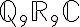 중 하나, 계수
중 하나, 계수
에서,
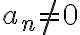 일 때,
일 때,
=n) : 차수
: 차수
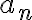 : 최고차항의 계수
: 최고차항의 계수
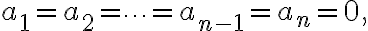 즉
즉 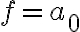 일 때
일 때  는 상수다항식.
는 상수다항식.
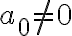 이면
이면  의 차수는 0
의 차수는 0
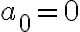 이면
이면  의 차수는 -∞이며
의 차수는 -∞이며  는 영다항식.
는 영다항식.
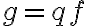 만족시키면
만족시키면  가
가 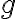 를 나눈다고 하며
를 나눈다고 하며 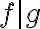 로 나타냄. 이 때
로 나타냄. 이 때
 는
는 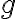 의 약다항식
의 약다항식
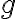 는
는  의 배다항식
의 배다항식
나눗셈정리 - 몫과 나머지가 유일하게 존재한다는..
나머지정리 -=0) 이면
이면 =(x-c)q(x)) 를 만족하는
를 만족하는 ) 가 유일하게 존재
가 유일하게 존재
최대공약다항식
기약다항식 - 곱으로 나타낼 수 없을 때..
다항식의 인수분해 정리 - 다항식은 기약다항식들의 곱으로 표시되고 그 표시 방법은 유일..
근본다항식 - 계수들을 모두 나누는 정수가 ±1 뿐일 때
가우스의 정리 - 다항식의 기약성에 관한
}
{
다항식
나머지정리 -
최대공약다항식
기약다항식 - 곱으로 나타낼 수 없을 때..
다항식의 인수분해 정리 - 다항식은 기약다항식들의 곱으로 표시되고 그 표시 방법은 유일..
근본다항식 - 계수들을 모두 나누는 정수가 ±1 뿐일 때
가우스의 정리 - 다항식의 기약성에 관한
}
계산 알고리즘 - Horner's method ¶
호너_방법? Horner_method
다항식
=a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0)
의 값을 계산(calculation, evaluation)할 때 연산을 줄이는 방법.
다음과 같이 변형하여 가장 안쪽 괄호부터 계산.
=(\cdots((a_n x + a_{n-1})\times x + a_{n-2})\times x + \cdots + a-1)\times x + a_0)
단순한 방법으로는
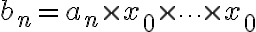 (곱셈
(곱셈  번)
번)
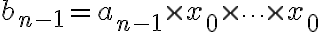 (곱셈
(곱셈  번)
번)
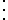
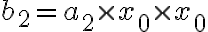 (곱셈 2번)
(곱셈 2번)
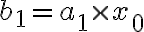 (곱셈 1번)
(곱셈 1번)
=b_n+b_{n-1}+\cdots+b_1+a_0)
호너 방법으로는
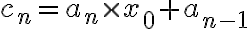
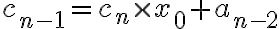
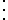
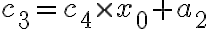
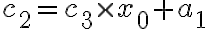
=c_2\times x_0+a_0)
이렇게 연산하게 되므로,
다항식
다음과 같이 변형하여 가장 안쪽 괄호부터 계산.
단순한 방법으로는 덧셈  번과 곱셈
번과 곱셈 /2) 번,
번,
호너 방법으로는 덧셈 곱셈 각각 번.
번.
호너 방법으로는 덧셈 곱셈 각각
(컴퓨터 알고리즘, 박정호)
다만 MW에서 쓰는 용어는 https://mathworld.wolfram.com/HornersRule.html 이다. https://mathworld.wolfram.com/HornersMethod.html 가 아니고.

