Laplace's equation

curr tmp goto
방정식,equation#s-11 Poisson and Laplace
방정식,equation#s-12 Poisson
방정식,equation#s-13 Laplace

다음 방정식

$\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}=0$

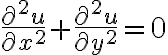
은 Pierre Laplace의 이름을 따 라플라스 방정식이라 하며 이것의 해를 조화함수라 한다. 이것은 heat_conduction (열,heat 전도,conduction), fluid_flow (유체,fluid 흐름,flow) and 전위,electric_potential 문제에서 역할이 있다(play a role).
(Stewart 9e)

//from 수학백과
라플라스 연산자(라플라시안,Laplacian)를 취했을 때, 0이 되는 함수,function를 찾는 방정식.

라플라스 방정식의 해,solution인 함수는 조화함수,harmonic_function.

차원,dimension에 따라, (=0이 되는 LHS는 ???) 다음과 같이 표시.

(2차원) $\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}$
(2차원) $\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2}$
(n차원) $\nabla^2 u = \frac{\partial^2 u}{\partial x_1^2} + \frac{\partial^2 u}{\partial x_2^2} + \cdots + \frac{\partial^2 u}{\partial x_n^2}$

//from wpen
Laplace DE는 "(a particular case of the Helmholtz equation)". [1]
라플라스 방정식은 헬름홀츠_방정식,Helmholtz_equation의 특수한 경우이다.

Laplace DE는 푸아송_방정식,Poisson_equation의 특이한 경우이기도 함. =0인 간단한 경우??

//from wpko
라플라스 방정식의 해,solution : 조화함수,harmonic_function

QQQ
이름이 이런 이유가 Laplacian이 0이다 - 에서 온 거? or not?

[edit]