보통 빛을 쏴서 생긴 그림자에 비유. (무한히 먼 곳의 점광원 or 평면에서 나오는 모두 평행인 그런 광원(이름이?)?)
표기 (다음 네 줄은 같음. due to https://wikidocs.net/74698 CHK)
거리,distance의 계산과 관련.
projxy
x 위로의 y의 정사영
y의 x 위로의 정사영
projection of y onto x
각,angle 특히 교각(angle of intersection) 관련.x 위로의 y의 정사영
y의 x 위로의 정사영
projection of y onto x
거리,distance의 계산과 관련.
사영을 하는 대상:
벡터,vector
선분,line_segment
모든 figures, shapes,
점,point - ex. (3D공간에서) 점 (a,b,c)에서 xy평면에 수선을 내리면 ‘xy평면으로 P의 사영’은 좌표가 (a,b,0)인 점.
...
사영하여 그림자가 그 위에 만들어지는(?) 대상:
축,axis위로,
직선,line 위로,
평면,plane 위로,
등등
벡터,vector
선분,line_segment
모든 figures, shapes,
점,point - ex. (3D공간에서) 점 (a,b,c)에서 xy평면에 수선을 내리면 ‘xy평면으로 P의 사영’은 좌표가 (a,b,0)인 점.
...
사영하여 그림자가 그 위에 만들어지는(?) 대상:
축,axis위로,
직선,line 위로,
평면,plane 위로,
등등
mklink
사영공간,projective_space - sub? 작성중
사영평면,projective_plane - 작성중
내적,inner_product
스칼라곱,scalar_product,dot_product
사영공간,projective_space - sub? 작성중
사영평면,projective_plane - 작성중
내적,inner_product
스칼라곱,scalar_product,dot_product
2. 스칼라사영 scalar projection ¶
The scalar projection of 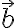 onto
onto 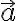
AKA the component of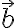 along
along 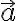
AKA the component of
기호: 
식
)
에서, 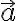 와
와 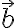 의 내적을
의 내적을
다음 식에서
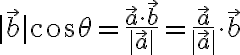
이므로, 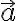 방향의 단위벡터와
방향의 단위벡터와 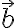 의 내적으로 계산할 수 있다.
의 내적으로 계산할 수 있다.
(a의 길이) × (b에서 a 위로의 스칼라사영)
으로 해석할 수 있음을 볼 수 있다.다음 식에서
(Stewart)
3. 스칼라사영과 벡터사영 ¶
Scalar projection of 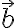 onto
onto 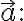
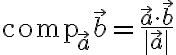
Vector projection of 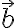 onto
onto 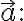
 \frac{\vec{a}}{|\vec{a}|} = \frac{\vec{a}\cdot\vec{b}}{|\vec{a}|^2} \vec{a})
보다시피, 벡터사영은 스칼라사영 곱하기 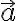 방향으로의 단위벡터,unit_vector와 같다.
방향으로의 단위벡터,unit_vector와 같다.
4. 정사영 ¶
'정'의 뜻이, 사영 중에서 '수직 orthogonal perpendicular 한 특별한 경우' 맞음? AKA 직교사영, 수직사영?
밀접, 비교: 성분,component(esp. 한 벡터에서 다른 벡터의 성분)
6. Misc ¶
벡터 및 선형대수 관련 문서를 읽다 보면 "정사영(projection)"이라는 표현이 엄청 자주 보이는데, 이것은 영단어 하나를 생략해 간단히 표시한 것이다. (엄밀히 말하면 틀렸다고 볼 수도 있고, 사영의 의미 중에서 다른 사영은 무시하고 임시로 정사영으로만 의미를 한정했다고 볼 수도 있다.) 명확하게 표현하면 둘은 각각,
사영 = projection
정사영 = orthogonal projection (= 직교사영)
이다.정사영 = orthogonal projection (= 직교사영)
사영보다 마이너하지만 '투영' 표현도 쓰임.
2023-11-05
projection의 번역으로 '투상'이라는 표현도 보임, 혹시 상은 image? 한자 chk. / 투상
투상  투상 https://ko.wikipedia.org/wiki/투상 ... via https://jebae.github.io/z-buffer
투상 https://ko.wikipedia.org/wiki/투상 ... via https://jebae.github.io/z-buffer
projection의 번역으로 '투상'이라는 표현도 보임, 혹시 상은 image? 한자 chk. /
8. bmks en ¶
Active Calculus(online free textbook) Subsection 9.3.5: Projections
https://activecalculus.org/multi/S-9-3-Dot-Product.html#S-9-3-Dot-Product-8
https://activecalculus.org/multi/S-9-3-Dot-Product.html#S-9-3-Dot-Product-8
10. MKL idempotence / idempotency ¶
projection operation is idempotent ... 한번 하든 두번 하든 같으므로.... 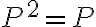 .... 항상? chk.
.... 항상? chk.
see also https://planetmath.org/idempotency
see also https://planetmath.org/idempotency
Twins:
https://everything2.com/title/Projection
https://ratsgo.github.io/linear algebra/2017/10/20/projection/
https://planetmath.org/idempotency (벡터공간,vector_space의 사영. 마지막 문장. - idempotency 설명에서)
https://encyclopediaofmath.org/wiki/Projection
https://everything2.com/title/Projection
https://ratsgo.github.io/linear algebra/2017/10/20/projection/
https://planetmath.org/idempotency (벡터공간,vector_space의 사영. 마지막 문장. - idempotency 설명에서)
https://encyclopediaofmath.org/wiki/Projection
2023-12-17
뜻이 다양한데 투영,projection페이지를 나누는 방법도 있을 듯
 Projection = https://simple.wikipedia.org/wiki/Projection
Projection = https://simple.wikipedia.org/wiki/Projection
뜻이 다양한데 투영,projection페이지를 나누는 방법도 있을 듯
Up:
기하학,geometry See that page. 저기에 관련 내용 있는데 합칠 예정. TOMERGE
벡터,vector의 주제임
선형변환,linear_transformation? chk
연산,operation / 연산자,operator ? chk
벡터,vector의 주제임
선형변환,linear_transformation? chk
연산,operation / 연산자,operator ? chk


![[https]](/123/imgs/https.png)