AKA 일차변환, 선형사상,linear_map
Sub:
직교변환,orthogonal_transformation - 직교성,orthogonality 선형변환? chk
bounded_linear_transformation
// 이하 sub임. via BigBook p196-199
영변환 zero_transformation=\vec{0})
항등변환 identity_transformation=\vec{v})
행렬변환 matrix_transformation=A\vec{x})
정사영,orthogonal_projection - curr at 사영,projection
사영,projection도? chk
모든 선형변환은 행렬변환으로 나타낼 수 있다. p199
bounded_linear_transformation
// 이하 sub임. via BigBook p196-199
영변환 zero_transformation
항등변환 identity_transformation
행렬변환 matrix_transformation
정사영,orthogonal_projection - curr at 사영,projection
사영,projection도? chk
모든 선형변환은 행렬변환으로 나타낼 수 있다. p199
1. 정의 ¶
벡터공간,vector_space 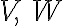 가 있고,
가 있고,
사상,map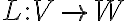 가 임의의 벡터,vector
가 임의의 벡터,vector 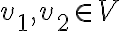 와 임의의 스칼라,scalar
와 임의의 스칼라,scalar  에 대해 다음 두 조건을 만족하면
에 대해 다음 두 조건을 만족하면 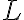 을
을 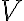 에서
에서 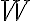 로의 선형변환이라고 한다.
로의 선형변환이라고 한다.
=L(v_1)+L(v_2))
=kL(v_1))
특히, V에서 V자신으로의 선형변환 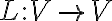 를 V위의 선형연산자(linear operator)라고 한다. 선형연산자,linear_operator
를 V위의 선형연산자(linear operator)라고 한다. 선형연산자,linear_operator
사상,map
2. 성질 ¶
V, W가 벡터공간이고 L:V→W을 선형변환이라 하면 다음이 성립한다.
(1) L(0)=0
(2) ∀v∈V, L(-v)=-L(v)
(3) ∀v, w∈V, L(v-w)=L(v)-L(w)
(2) ∀v∈V, L(-v)=-L(v)
(3) ∀v, w∈V, L(v-w)=L(v)-L(w)
3. 일차변환의 예 ¶
| x방향 확대 | ||
| y방향 확대 | ||
| x방향 전단 | ||
| y방향 전단 | ||
| x축 반전 | ||
| y축 반전 | ||
| 원점 중심으로 45° 회전 | ||
| 임의의 각도 θ만큼 회전 | ||
| 평면 전체를 직선으로 압축 |
4. Invertible Linear Transformations ¶
A linear transformation 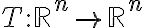 is said to be invertible if there exists a function
is said to be invertible if there exists a function  such that
such that
)=\vec{x},\,T(S(\vec{x}))=\vec{x}\;\;\forall\vec{x}\in\mathbb{R}^n)
이 때 S는 inverse of T, 즉 T-1이다.
(Lay, 2.3)
5. (TBW) 선형변환과 행렬의 관계 ¶
from namuwiki/행렬
선형대수학의_기본정리에 따르면, 모든 선형변환은 행렬,matrix로 표현 가능하고 그 역도 성립한다. 행렬,matrix#s-17 ("행렬과 일차변환")에 내용 있음.
선형대수학의_기본정리에 따르면, 모든 선형변환은 행렬,matrix로 표현 가능하고 그 역도 성립한다. 행렬,matrix#s-17 ("행렬과 일차변환")에 내용 있음.
See also ![[https]](/123/imgs/https.png) 수학백과: 일차변환
수학백과: 일차변환
{
TBW:
일차변환과 행렬,matrix의 관계
일차변환의 합성,composition과 행렬곱셈matrix_multiplication의 관계
}
![[https]](/123/imgs/https.png) 수학백과: 일차변환
수학백과: 일차변환{
TBW:
일차변환과 행렬,matrix의 관계
일차변환의 합성,composition과 행렬곱셈matrix_multiplication의 관계
}
Transformations and Matrices : 2D transformation (interactive app, 행렬 숫자를 바꿔가면서 어떻게 되는지 볼 수 있음)
https://www.mathsisfun.com/algebra/matrix-transform.html
https://www.mathsisfun.com/algebra/matrix-transform.html
선형변환을 행렬로 표현하는 것에 대해.
6. tmp links ko ¶
네 근본적 부분공간,subspace
https://angeloyeo.github.io/2020/11/17/four_fundamental_subspaces.html
{
선형변환의
입력(정의역,domain)은 행공간,row_space과 영공간,null_space의 합집합.
출력(치역,range)은 열공간,column_space.
} CHK
https://angeloyeo.github.io/2020/11/17/four_fundamental_subspaces.html
{
선형변환의
입력(정의역,domain)은 행공간,row_space과 영공간,null_space의 합집합.
출력(치역,range)은 열공간,column_space.
} CHK
chk: 선형변환이 아닌 변환은 모두 비선형변환?
관련:
선형성,linearity
사영,projection and 정사영(orthogonal projection)
영변환(zero transformation)
항등변환(identity transformation)
행렬변환(matrix transformation)
선형성,linearity
사영,projection and 정사영(orthogonal projection)
영변환(zero transformation)
항등변환(identity transformation)
행렬변환(matrix transformation)
tmp bmks ko
https://chocobear.tistory.com/113 선형변환
https://chocobear.tistory.com/115 (del ok) 선형변환의 성질 중 하나를 알아봄 - with rank-nullity_theorem(= dimension_theorem)
https://chocobear.tistory.com/116 선형변환의 행렬 표현 - matrix_representation. 순서기저,ordered_basis 정의한 다음.
https://chocobear.tistory.com/113 선형변환
https://chocobear.tistory.com/115 (del ok) 선형변환의 성질 중 하나를 알아봄 - with rank-nullity_theorem(= dimension_theorem)
https://chocobear.tistory.com/116 선형변환의 행렬 표현 - matrix_representation. 순서기저,ordered_basis 정의한 다음.
Ref.
정의:![[http]](/123/imgs/http.png) http://matrix.skku.ac.kr/sglee/linear/ocu/20701.html
http://matrix.skku.ac.kr/sglee/linear/ocu/20701.html
성질:![[http]](/123/imgs/http.png) http://matrix.skku.ac.kr/sglee/linear/ocu/20702.html
http://matrix.skku.ac.kr/sglee/linear/ocu/20702.html
정의:
![[http]](/123/imgs/http.png) http://matrix.skku.ac.kr/sglee/linear/ocu/20701.html
http://matrix.skku.ac.kr/sglee/linear/ocu/20701.html성질:
![[http]](/123/imgs/http.png) http://matrix.skku.ac.kr/sglee/linear/ocu/20702.html
http://matrix.skku.ac.kr/sglee/linear/ocu/20702.htmlTwins
https://mathworld.wolfram.com/LinearTransformation.html
https://everything2.com/title/linear transformation
https://planetmath.org/lineartransformation
https://proofwiki.org/wiki/Definition:Linear_Transformation
 Linear_map
Linear_map
 선형_변환
선형_변환
https://encyclopediaofmath.org/wiki/Linear_operator - linear transformation, linear map
https://encyclopediaofmath.org/wiki/Linear_transformation
https://mathworld.wolfram.com/LinearTransformation.html
https://everything2.com/title/linear transformation
https://planetmath.org/lineartransformation
https://proofwiki.org/wiki/Definition:Linear_Transformation
https://encyclopediaofmath.org/wiki/Linear_operator - linear transformation, linear map
https://encyclopediaofmath.org/wiki/Linear_transformation

