Ax=0을 만족하는 A 집합을 Nul A 라고 한다. (A의 영공간)
The null space of a matrix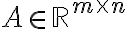 is the set of all solutions of a homogeneous linear system, Ax=0.
is the set of all solutions of a homogeneous linear system, Ax=0.
The null space of a matrix
ㄷㄱㄱ Week 5-1 ¶
방정식
\vec{x}=\vec{0})
의 모든 해,solution의 집합,set은 행렬,matrix ) 의 영공간,null_space이며, (영공간을 이루며?)
의 영공간,null_space이며, (영공간을 이루며?)
 에 대응하는
에 대응하는  의 고유공간,eigenspace으로도 부른다.
의 고유공간,eigenspace으로도 부른다.
고유공간,eigenspace은 영벡터,zero_vector 및 (위 방정식을 만족하는 에 대응하는 모든 고유벡터,eigenvector들 )로 구성된다. - 번역chk
에 대응하는 모든 고유벡터,eigenvector들 )로 구성된다. - 번역chk
고유공간,eigenspace은 영벡터,zero_vector 및 (위 방정식을 만족하는
(원문)
(𝐴 − 𝜆𝐼)𝐱 = 𝟎
The set of all solutions of the above equation is the null space of the matrix (𝐴 − 𝜆𝐼), which we call the eigenspace of 𝐴 corresponding to 𝝀.
The eigenspace consists of the zero vector and all the eigenvectors corresponding to 𝜆, satisfying the above equation.
(𝐴 − 𝜆𝐼)𝐱 = 𝟎
The set of all solutions of the above equation is the null space of the matrix (𝐴 − 𝜆𝐼), which we call the eigenspace of 𝐴 corresponding to 𝝀.
The eigenspace consists of the zero vector and all the eigenvectors corresponding to 𝜆, satisfying the above equation.
정의: 행렬 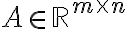 의 영공간,null_space은 homogeneous_linear_system(동차선형계? curr. 선형계,linear_system)
의 영공간,null_space은 homogeneous_linear_system(동차선형계? curr. 선형계,linear_system) 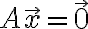 의 모든 해들의 집합이다.
의 모든 해들의 집합이다.
 의 영공간을
의 영공간을 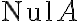 라고 표기한다.
라고 표기한다.
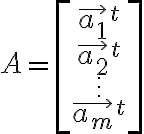 에 대하여,
에 대하여, 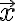 는 다음 조건을 만족해야 한다.
는 다음 조건을 만족해야 한다.
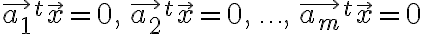
다시 말해, 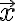 는
는  안의 모든 행벡터,row_vector에 직교해야 한다. (should be orthogonal to) // 직교성,orthogonality
안의 모든 행벡터,row_vector에 직교해야 한다. (should be orthogonal to) // 직교성,orthogonality
(원문)
Definition: The null space of a matrix 𝐴 ∈ ℝ𝑚×𝑛 is the set of all solutions of 𝐴𝐱 = 𝟎 called a homogeneous linear system.
We denote the null space of 𝐴 as Nul 𝐴.
For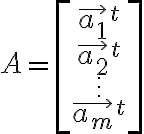
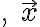 should satisfy the following:
should satisfy the following:
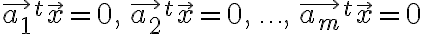
That is, 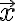 should be orthogonal to every row vector in
should be orthogonal to every row vector in 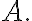
Definition: The null space of a matrix 𝐴 ∈ ℝ𝑚×𝑛 is the set of all solutions of 𝐴𝐱 = 𝟎 called a homogeneous linear system.
We denote the null space of 𝐴 as Nul 𝐴.
For
영공간은 부분공간
정리: 행렬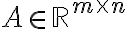 의 영공간,null_space은
의 영공간,null_space은  의 부분공간,subspace이다. 다른 말로 하면, 연립방정식
의 부분공간,subspace이다. 다른 말로 하면, 연립방정식 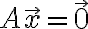 의 모든 해의 집합은
의 모든 해의 집합은  의 부분공간이다.
의 부분공간이다.
Note: 그래서 고유공간,eigenspace은 특정한 차원,dimension의 기저,basis 벡터 집합을 갖는다. - 차원과 기저 벡터 개수가 같다는거? 번역chk
정리: 행렬
Note: 그래서 고유공간,eigenspace은 특정한 차원,dimension의 기저,basis 벡터 집합을 갖는다. - 차원과 기저 벡터 개수가 같다는거? 번역chk
(원문)
Null Space is a Subspace
Theorem: The null space of a matrix 𝐴 ∈ ℝ𝑚×𝑛 is a subspace of ℝ𝑛. In other words, the set of all the solutions of a system 𝐴𝐱 = 𝟎 is a subspace of ℝ𝑛.
Note: An eigenspace thus have a set of basis vectors with a particular dimension.
Null Space is a Subspace
Theorem: The null space of a matrix 𝐴 ∈ ℝ𝑚×𝑛 is a subspace of ℝ𝑛. In other words, the set of all the solutions of a system 𝐴𝐱 = 𝟎 is a subspace of ℝ𝑛.
Note: An eigenspace thus have a set of basis vectors with a particular dimension.
MathWorld 설명 ¶
https://mathworld.wolfram.com/NullSpace.html
{
 의 선형변환,linear_transformation중 하나를
의 선형변환,linear_transformation중 하나를 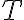 라 하면,
라 하면,
영공간 Null(T) 혹은 Ker(T)는,
다음을 만족하는 모든 벡터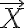 들의 집합이다.
들의 집합이다.
=\vec{0})
i.e.
\equiv\left\lbrace \vec{X} : T(\vec{X})=\vec{0} \right\rbrace.)
}
{
영공간 Null(T) 혹은 Ker(T)는,
다음을 만족하는 모든 벡터
핵,kernel ¶
핵,kernel은 동의어 같은데 뉘앙스 차이가 있다면 적을 것.
관련 - nullity, rank, rank nullity thm
https://artofproblemsolving.com/wiki/index.php/Kernel
여기는 집합론,set_theory와 추상대수학 abstract_algebra의 kernel 얘기. 첫문장: "In general, a kernel is a measure of the failure of a homomorphism to be injective." // 준동형사상,homomorphism 단사,injection
여기는 집합론,set_theory와 추상대수학 abstract_algebra의 kernel 얘기. 첫문장: "In general, a kernel is a measure of the failure of a homomorphism to be injective." // 준동형사상,homomorphism 단사,injection
AKA 해공간 ¶
https://wikidocs.net/76882 2. 에 의하면 뉘앙스가 약간 다른가? 영공간은 행렬에 대한, 해공간은 방정식에 대한... 이게 옳은듯? (물론 행렬과 방정식계는 equivalent하므로 구분이 별 의미는 없지만 뉘앙스가..)
{
행렬![$A=[a_{ij}]_{m\times n}$ $A=[a_{ij}]_{m\times n}$](/123/cgi-bin/mimetex.cgi?\Large A=[a_{ij}]_{m\times n}) 에 대해 집합
에 대해 집합
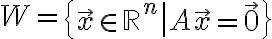
은  의 부분공간,subspace이다. 이러한
의 부분공간,subspace이다. 이러한 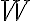 를
를
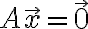 의 해공간(solution space) 또는
의 해공간(solution space) 또는
 의 영공간(null space)이라 하며
의 영공간(null space)이라 하며
기호로 Null(A)로 나타낸다.
{
행렬
Ax=0은 A를 계수행렬로 하는 동차 선형연립방정식이고, 그 해를 다 모아놓은 것을 해공간이라 한다.
tmp ¶
mklink:
영부분공간,zero_subspace과 관계가?
{
영공간은 null space라고 하는데 반해,
영부분공간은 null subspace라고 안하고 zero subspace라 하는데 이유가??
영부분공간,zero_subspace과 관계가?
{
영공간은 null space라고 하는데 반해,
영부분공간은 null subspace라고 안하고 zero subspace라 하는데 이유가??
Twins:
![[https]](/123/imgs/https.png) 수학백과: 영화공간
수학백과: 영화공간
https://proofwiki.org/wiki/Definition:Null_Space
https://mathworld.wolfram.com/NullSpace.html
![[https]](/123/imgs/https.png) 수학백과: 영화공간
수학백과: 영화공간https://proofwiki.org/wiki/Definition:Null_Space
https://mathworld.wolfram.com/NullSpace.html
twins minor:
https://everything2.com/title/null space
http://mlwiki.org/index.php/Nullspace - 강의 노트 형식
https://everything2.com/title/null space
http://mlwiki.org/index.php/Nullspace - 강의 노트 형식

