야코비안,Jacobian

야코비 행렬 Jacobian matrix
야코비 행렬식 Jacobian determinant - 간단히 야코비안 Jacobian (Thomas)

각각 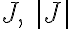$J,\ |J|$ ??



편미분의 연쇄법칙과 관련?
see 편미분,partial_derivative#s-4
다변수함수의 chain rule과 관련.
연쇄법칙,chain_rule



[edit]

1. 표기 notation


$\frac{\partial(f,g)}{\partial(u,v)}$ : Jacobian of $f\textrm{ and }g$ with respect to $u\textrm{ and }v$

(O'Neil AEM 7e)

[edit]

2. 한국어 설명

직교 uv평면에 있는 영역 G에서
$\downarrow \;\; x=g(u,v),\, y=h(u,v)$ 치환으로
직교 xy평면에 있는 영역 R로 일대일 변환이 이루어 진 상황을 가정.
R은 변환에 의한 G의 상,image이며 G는 R의 원상,preimage이라고 한다.
R에서 정의된 임의의 함수 $f(x,y)$ 는 G에서 정의된 함수 $f(g(u,v),h(u,v))$ 로 생각할 수 있다.
R 위에서의 적분 계산을 G 위에서의 적분 계산으로 바꿀 수 있음.
R 위에서 $f(x,y)$ 의 적분과 G 위에서 $f(g(u,v),h(u,v))$ 의 적분과는 어떤 관계가 있을까?

...(fill in this later)

좌표변환,coordinate_transformation $x=g(u,v),\,y=h(u,v)$ 의 야코비 행렬식(Jacobian determinant) 또는 간단히 야코비안(Jacobian)은 다음과 같다.
$J(u,v)=\left|\begin{matrix}\frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}\\\frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}\end{matrix}\right|={\partial x\over \partial u}{\partial y\over \partial v}-{\partial y\over \partial u}{\partial x\over \partial v}$
야코비안은
$J(u,v)=\frac{\partial(x,y)}{\partial(u,v)}$
로 쓰기도 한다.
야코비안은 변환에 의해 $(u,v)$ 주변의 넓이가 얼마나 확대되는지 혹은 축소되는지를 나타내는 척도이다.

(Thomas 13e ko chap13.8 중적분에서의 변수변환)

자코비안(Jacobian) 행렬의 기하학적 의미
https://angeloyeo.github.io/2020/07/24/Jacobian.html
행렬,matrix, 변환,transformation과 연관해 설명.

from https://suhak.tistory.com/944
일변수 함수를 적분할 때의 치환적분,integration_by_substitution의 방법과 마찬가지로, 이변수 함수를 적분할 때 변수를 바꿀 일이 많다. 이 때는 치환,substitution보다는 변환,transformation이라는 용어를 쓴다.
xy좌표 ↔ uv좌표 변환 식이 이렇고
$x=f(u,v),\;y=g(u,v)$
x,y,u,v가 모두 t의 함수라면 연쇄법칙,chain_rule에 따라
$\frac{dx}{dt}=\frac{\partial f}{\partial u}\frac{du}{dt}+\frac{\partial f}{\partial v}\frac{dv}{dt},$
$\frac{dy}{dt}=\frac{\partial g}{\partial u}\frac{du}{dt}+\frac{\partial g}{\partial v}+\frac{dv}{dt}$
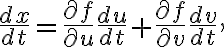
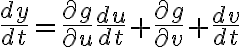
이렇고 미분,differential을 생각하면
$dx=\frac{\partial f}{\partial u}du+\frac{\partial f}{\partial v}dv,$
$dy=\frac{\partial g}{\partial u}du+\frac{\partial g}{\partial v}dv$
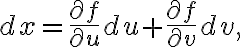
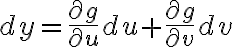
이렇고, 이것을 행렬로 표현하면
$\begin{bmatrix}dx\\dy\end{bmatrix}=\begin{bmatrix}\frac{\partial f}{\partial u}&\frac{\partial f}{\partial v}\\ \frac{\partial g}{\partial u}&\frac{\partial g}{\partial v}\end{bmatrix}\begin{bmatrix}du\\dv\end{bmatrix}$
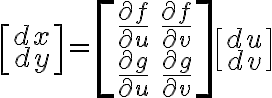
위의 coefficient matrix를 Jacobian matrix라고 하고, 그 행렬식을 보통 Jacobian이라 한다.
$J(u,v)=\frac{\partial(f,g)}{\partial(u,v)}=\begin{vmatrix}\frac{\partial f}{\partial u}&\frac{\partial f}{\partial v}\\ \frac{\partial g}{\partial u}&\frac{\partial g}{\partial v}\end{vmatrix}$

[edit]

3. 영어 설명


[edit]

4. tmp

[edit]

5. tmp 이정일

Jacobian

$J\left(\frac{x,y}{r,\theta}\right)=\left|\begin{array}{cc}\frac{\partial x}{\partial r}&\frac{\partial x}{\partial\theta}\\\frac{\partial y}{\partial r}&\frac{\partial y}{\partial \theta}\end{array}\right|=\left|\begin{array}{cc}\cos\theta&-r\sin\theta\\\sin\theta&r\cos\theta\end{array}\right|=r\cos^2\theta+r\sin^2\theta=r$

$\int dx\int dyf(x,y)=\int dr\int d\theta \underline{r} f(r\cos\theta,r\sin\theta)$
(r is Jacobian)

if there is another symmetry
$\int drd\theta r f(r,\theta)$
$=\int dr r \int d\theta f(r)$
$=\int dr [r f(r)]\int_0^{2\pi}d\theta$
$=\int dr [2\pi rf(r)]$
$=\int (dr)(2\pi r)[f(r)]$ -- user 2017-12-17 04:27:51

[edit]

6. tmp bmks ko

from Namu:야코비안, at 2020-10-31, chk
{
Related:
좌표계 변환 - 좌표계,coordinate_system 변환,transformation
다중적분 - 중적분,multiple_integral curr goto 적분,integration
미분소 - goto 미분,differential
행렬식,determinant

다중적분을 할 때, 미분소를 같은 차원의 좌표계로 변환하는 데 쓰는 행렬식.

$J = \begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta} \end{vmatrix} = \left| \dfrac{\partial (x, \ y)}{\partial (r, \ \theta)}\right|$
}
야코비 행렬 혹은 자코비 행렬이란? Jacobian Matrix
https://freshrimpsushi.tistory.com/989
https://freshrimpsushi.github.io/posts/jacobian-matrix/
"전 도함수total_derivative라고도 하며, 다변수 벡터함수의 도함수를 의미한다." - 전미분,total_derivative

곡선 좌표계에서 좌표 변환과 야코비안 The Coordinate Transform and Jacobian
https://freshrimpsushi.tistory.com/1806
https://freshrimpsushi.github.io/posts/the-coordinate-transform-and-jacobian/
좌표,coordinate 좌표변환,coordinate_transformation
https://t-robotics.blogspot.com/2013/12/jacobian.html
robotics, 로봇자세제어, kinematics 연관지어 설명
중간에 관절공간 joint_space(or configuration_space), 회전행렬,rotation_matrix에 대한 links 있음

[edit]

7. tmp videos ko

[edit]

8. tmp videos en

What is Jacobian? | The right way of thinking derivatives and integrals - YouTube (Mathemaniac)
https://www.youtube.com/watch?v=wCZ1VEmVjVo&t=1110s

[edit]

9. 평형, 안정성과 Jacobian

[edit]

10. addhere

[edit]

11. addhere


AKA 자코비안

독일인 Carl Gustav Jacob Jacobi (1804-1851)의 이름을 따서 명명됨.

Twins:
WpKo:야코비_행렬
WpEn:Jacobian_matrix_and_determinant
Namu:야코비안
https://mathworld.wolfram.com/Jacobian.html
https://everything2.com/title/Jacobian Matrix
[https]수학백과: 야코비 행렬
{
"직선을 직선으로 보내는 일변수함수의 미분은 일차근사식에서 일차항의 계수이다. 평면에서 평면으로 가는 평면변환의 미분은 이 평면변환의 일차근사식에서 일차항의 계수에 해당하는 행렬로 주어진다."
일변수함수의 미분 직선 → 직선 일차근사식에서 일차항의 계수
평면변환의 미분 평면 → 평면 평면변환의 일차근사식에서 일차항의 계수에 해당하는 행렬
}
[https]수학백과: 야코비 행렬식
{
야코비_행렬,Jacobian_matrix의 행렬식,determinant.
역함수,inverse_function를 구하거나 치환적분,integration_by_substitution을 할 때 사용.
}

Up:
선형대수,linear_algebra? 행렬,matrix?
행렬식,determinant